Dirichlet-regression
Die Dirichlet-Regression zielt auf die Vorhersage von Zusammensetzungsdaten ab und kann in vielen Bereichen wie Ökologie, Gesundheit und Wirtschaft eingesetzt werden. Verfügbar in Excel mit der XLSTAT Software.
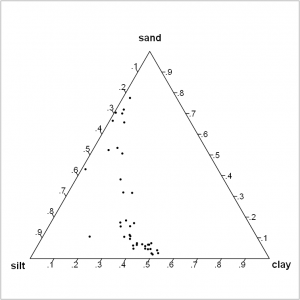
Wofür wird die Dirichlet-Regression verwendet?
Wie die lineare Regression oder die logistische Regression zielt die Dirichlet-Regression darauf ab, Vorhersagen auf der Grundlage einer oder mehrerer erklärender Variablen zu treffen. Im Gegensatz zu vielen anderen Typen von Regressionsanalysen sagt ein Dirichlet-Regressionsmodell jedoch nicht bestimmte Werte einer erklärenden Variablen voraus, sondern mehrere Anteile von Zusammensetzungsdaten. In diesem Sinne handelt es sich um eine Verallgemeinerung der Beta-Regression, die nur die Vorhersage von zwei Anteilen ermöglicht.
Wann sollte man die Dirichlet-Regression verwenden?
Wenn es sich bei Ihren Antwortvariablen handelt, beispielsweise um Anteile von Baumarten, kann die Dirichlet-Regression es Ihnen ermöglichen, den Anteil von Eichen, Apfelbäumen und Birken in Abhängigkeit von Variablen, wie der durchschnittlichen Lufttemperatur und der durchschnittlichen Luftfeuchtigkeit, in verschiedenen geografischen Zonen vorherzusagen.
Wie funktioniert die Dirichlet-Regression in XLSTAT?
Die in XLSTAT-R entwickelte Funktion der Dirichlet-Regression ruft die Funktion DirichReg aus dem Paket DirichletReg in R (Marco Johannes Maier) auf, die mehrere Optionen bietet, die Ihnen einen tiefen Einblick in Ihre Daten ermöglichen:
- Wählen Sie mehrere Spalten aus, die die Anteile der einzelnen zu erklärenden Variablen enthalten
- Wählen Sie mehrere erklärende quantitative Variablen
- Berücksichtigen Sie Wechselwirkungen zwischen Ihren Daten
- Wählen Sie zwischen dem üblichen und dem alternativen Mittelwert-/Ausbreitungsmodell
- Visualisieren Sie die Verteilung Ihrer Daten mit einem ternären Diagramm
Was ist der Unterschied zwischen Dirichlet-Regression, Beta-Regression und linearer Regression?
Was ist eine lineare Regression?
Im Gegensatz zur Dirichlet-Regression und zur Beta-Regression werden bei der linearen Regression keine Proportionen vorhergesagt. Sie besteht in der Vorhersage einer quantitativen Variablen auf der Grundlage einer oder mehrerer anderer quantitativer Variablen und geht davon aus, dass zwischen den Variablen eine lineare Beziehung besteht. Hier ist die Gleichung des linearen Regressionsmodells:
Y=X*β + ε
Dabei ist Y der Vektor der Werte der vorhergesagten Variablen, X der Vektor (oder die Matrix) der Werte der erklärenden Variable(n), β der Vektor der Regressionskoeffizienten und ε der Zufallsfehler. Wenn Sie mehr über die lineare Regression in XLSTAT wissen möchten, zögern Sie nicht, dieses Feature zu lesen.
Was ist die Beta-Regression?
Die Beta-Regression wird benutzt, um die Wahrscheinlichkeiten des Eintretens eines Ereignisses (und dessen Gegenteil) vorherzusagen. Sie setzt voraus, dass die Antwortvariable einer Beta-Verteilung folgt: Y ~ B(μ,φ) mit mu dem Mittelwert und phi einem Präzisionsparameter, sodass p=μ*φ ein Formparameter ist. Wir müssen diese Parameter anhand unserer Daten schätzen. Dazu verwenden wir für jede Variable y_t eine Verknüpfungsfunktion, sodass g(μ_t)=X*β+ε, und wenden die obige lineare Regressionsmethode an, um die Werte g(μ_t) zu ermitteln, die es uns ermöglichen, jeden μ_t und φ zu schätzen, bevor wir den Formparameter p finden.
Möchten Sie herausfinden, wann Sie die Beta-Regression verwenden sollten? Nehmen wir zum Beispiel an, dass wir für jeden deutschen Bürger die Wahrscheinlichkeit vorhersagen wollen, ob er gesund ist oder nicht, und zwar in Abhängigkeit von mehreren Faktoren wie Rauchen, Alkoholkonsum und durchschnittliche Schlafdauer. In diesem Fall wäre das Ereignis „gesund“, sein Gegenteil wäre „ungesund“, und wir würden versuchen, die Wahrscheinlichkeit zu schätzen, dass der Bürger gesund ist.
Was ist Dirichlet-Regression?
Was ist die Dirichlet-Regression? Die Dirichlet-Regression ist eine Verallgemeinerung der Beta-Regression. Anstatt nur eine Wahrscheinlichkeit oder einen Anteil vorherzusagen, kann sie mit einem ähnlichen Ansatz mehrere Anteile oder Wahrscheinlichkeiten für mehr als zwei Ergebnisse vorhersagen. Wir gehen davon aus, dass die Antwortvariable einer Dirichlet-Verteilung folgt, die der Beta-Verteilung ähnlich ist, aber mehr als ein Ereignis und sein Gegenteil berücksichtigt.
Wie oben beschrieben kann sie zur Vorhersage von Anteilen verschiedener Arten verwendet werden, könnte aber auch das Beispiel der Beta-Regression auf einen Gesundheitswert auf einer Skala von 1 bis 5 anstatt einfach „gesund“ oder „ungesund“ erweitern.

