Wie erstellt und validiert man multiple und einfache lineare Regressionen in XLSTAT?

Wenn es Ihnen wie den meisten Forschern und Datenanalysten geht, befinden Sie sich wahrscheinlich in Situationen, in denen Sie zukünftige Trends vorhersagen, die Schlüsselfaktoren, die ein Ergebnis beeinflussen, identifizieren oder einfach die Verbindung zwischen Variablen verstehen müssen. In diesen Fällen ist die lineare Regression ein unverzichtbares Werkzeug für jeden, der versucht, die Beziehungen innerhalb seiner Daten zu verstehen und auf der Grundlage dieses Wissens Vorhersagen zu treffen. Der Einstieg in die lineare Regression kann jedoch entmutigend sein, insbesondere für Anfänger in der statistischen Analyse. 

Hier sind einfach zu bedienende statistische Analysewerkzeuge wie XLSTAT und eine gründliche Ausbildung unerlässlich, um die Kluft zwischen dem Bedarf an fortgeschrittenen statistischen Methoden und der Leichtigkeit ihrer effektiven Anwendung zu überbrücken. 

In einem unserer Webinare hat Jean-Paul Maalouf, Berater für Datenwissenschaft, den Teilnehmern erklärt, wie und warum ein lineares Regressionsmodell verwendet wird und wie XLSTAT dabei helfen kann, häufige Fehler in dieser Art der Modellierung zu erkennen.  

Sehen Sie sich das Webinar an oder lesen Sie weiter, um zu erfahren, wie man einfache multiple lineare Regressionen in XLSTAT mit Dr. Maalouf erstellt und validiert. 

ÜBER XLSTAT STATISTISCHE SOFTWARE 

Da wir die Verwendung von XLSTAT für Ihre lineare Regressionsmodellierung diskutieren werden, kann es hilfreich sein, sich mit der allgemeinen Funktionalität dieser leistungsstarken Statistiksoftware vertraut zu machen. XLSTAT kann Ihnen dabei helfen, Ihre statistischen Analysen zu verbessern und zu rationalisieren, während Sie in Microsoft Excel arbeiten. XLSTAT stellt Ihnen über 300 Funktionen zur Analyse, Modellierung und Visualisierung von Daten zur Verfügung, die in verschiedene Kategorien von Werkzeugen unterteilt sind: 

• Deskriptiv - Erklärung einzelner Variablen oder Verbindungen zwischen zwei Variablen (z.B. Ermittlung des Mittelwertes oder der Standardabweichung in einem Datensatz) 
• Explorativ - Suche nach Mustern in großen Datensätzen
• Statistisches Testen - Analysieren von Daten zum Nachweis oder zur Widerlegung einer Hypothese
• Statistische Modellierung - Verstehen, wie sich eine Variable unter dem Einfluss anderer Variablen verhält, und dann Verwendung dieser Beziehung, die oft durch eine Regressionsgleichung ausgedrückt wird, um Vorhersagen zu treffen 
• Datenaufbereitung - Der Prozess der Aufbereitung von Rohdaten für die Analyse 
• Datenvisualisierung - Verwendung von Diagrammen und Tabellen zur Darstellung von Dateninformationen 
• Maschinelles Lernen - Nutzung von KI, um aus Daten zu lernen und Ergebnisse vorherzusagen 

Zusätzlich enthält XLSTAT fortgeschrittene Funktionen, die speziell für die Bereiche Sensorik, Marktforschung, Life Science und Qualität geeignet sind.  

In diesem Artikel werden wir uns auf statistische Tests und statistische Modellierung konzentrieren. Um mehr über diese anderen Funktionen von XLSTAT zu erfahren, besuchen Sie unsere Tutorien. 

WAS SIND STATISTISCHE MODELLIERUNG UND STATISTISCHE TESTS? 

Zunächst einmal ist ein statistisches Modell eine vereinfachte Darstellung der Realität anhand von Daten, die häufig eine Regressionsanalyse zur Ermittlung linearer Beziehungen beinhaltet. Mit Hilfe der statistischen Modellierung können wir verstehen, wie sich eine Variable verhält, wenn sich andere Variablen ändern. Sobald wir ein statistisches Modell haben, das sich als genau und nützlich erwiesen hat, können wir es verwenden, um anhand neuer Daten Vorhersagen über die Ergebnisse zu machen. 

Beim statistischen Testen werden statistische Modelle verwendet, um eine Hypothese zu beweisen oder zu widerlegen. Ganz allgemein ausgedrückt geht es beim statistischen Testen darum, festzustellen, ob sich Variable A signifikant verändert, wenn sie von Variable B beeinflusst wird: 

• Die Nullhypothese: Es gibt keine signifikante Veränderung der Variable A in Bezug auf die Variable B. 
• Alternativhypothese: Es gibt eine signifikante Veränderung der Variable A in Bezug auf die Variable B. 

Statistische Tests ergeben eine Zahl, die als Wahrscheinlichkeitswert (p-Wert) bezeichnet wird. Der p-Wert gibt an, wie wahrscheinlich es ist, dass die Nullhypothese zutrifft, d. h. wie wahrscheinlich es ist, dass es keine signifikante Veränderung gibt. Ein p-Wert ist eine Zahl zwischen 0 und 1 - je näher der Wert an 1 liegt, desto weniger signifikant ist das Ergebnis. Bei jedem statistischen Test müssen die Forscher ihren eigenen p-Wert-Grenzwert festlegen. 

WIE WÄHLE ICH EINE STATISTISCHE MODELLIERUNGSMETHODE FÜR MEINE DATEN? 

Es gibt viele, viele verschiedene Arten von statistischen Modellen. Welche Methode Sie wählen, hängt von den Daten ab, die Sie haben, und davon, was Sie darüber verstehen wollen. Dr. Maalouf erläuterte einige der gängigen Modellierungsmethoden für verschiedene Arten von Variablen. 

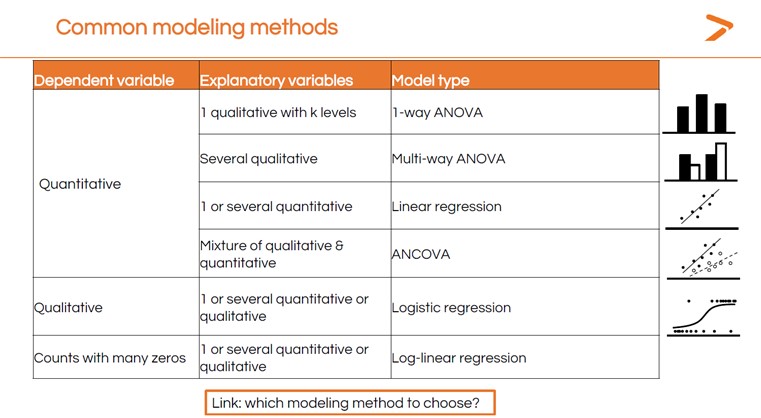
Bei so vielen Optionen kann es eine Herausforderung sein, den richtigen statistischen Test für Ihre Analyse zu wählen. Hier kann das Tool MyAssistant von XLSTAT helfen. Beantworten Sie einfach eine Reihe von Fragen, und MyAssistant wird Sie zum richtigen Test für Ihre Datenanalyse führen. Wir bieten auch einen kurzen Leitfaden zur statistischen Modellierung an, der Ihnen helfen kann, die richtige Modellierungsmethode in XLSTAT zu wählen, basierend auf Ihren Daten und dem Ziel Ihrer Analyse.  

WIE BESTIMME ICH, WELCHE VARIABLEN ABHÄNGIG ODER UNABHÄNGIG SIND? 

Zunächst sollten Sie die Frage, die Sie beantworten möchten, in Worte fassen. Im XLSTAT-Webinar erstellte Dr. Maalouf einen Beispieldatensatz, der die Software zur Verwaltung von Kundendaten (CRM) eines Online-Schuhhändlers darstellen sollte. Die Frage, die er untersuchen wollte, war: „Wie variiert der Rechnungsbetrag in Abhängigkeit von der vor Ort verbrachten Zeit?“ 

In diesem Beispiel ist die Variable, die Sie zu verstehen versuchen (der Rechnungsbetrag), die abhängige Variable. Die Variable, mit der Sie sie vergleichen (Zeit auf der Baustelle), ist die unabhängige Variable. 

EINSTIEG IN DIE LINEARE REGRESSIONSMODELLIERUNG: ERSTE VISUALISIERUNG 

Der erste Schritt bei der Durchführung einer linearen Regression mit XLSTAT besteht darin, sich einen schnellen Überblick über die Beziehung zwischen den abhängigen und unabhängigen Variablen zu verschaffen, indem Sie eine einfache Visualisierung erstellen. Dr. Maalouf empfiehlt die Erstellung eines Streudiagramms für diesen ersten Schritt. 

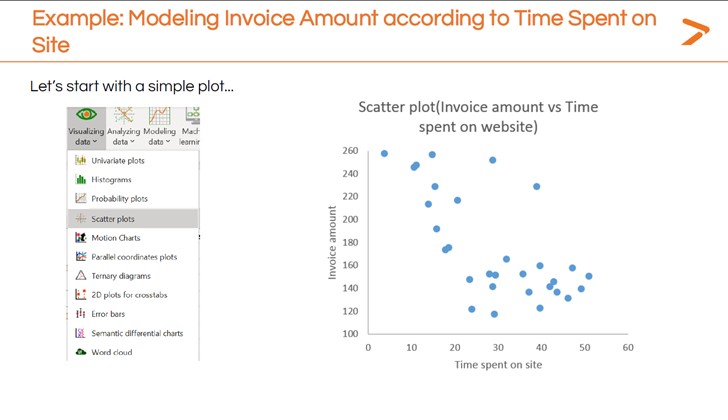
Um schnell ein Streudiagramm in XLSTAT zu erstellen 

• Klicken Sie auf das Icon „Visualisierung von Daten“ in der Toolbar 
• Wählen Sie „Streudiagramme“ aus dem Dropdown-Menü 
• In dem erscheinenden Dialogfenster definieren Sie die abhängigen (y-Achse) und unabhängigen (x-Achse) Variablen 
• Erzeugen Sie die Punktwolke 

Das erste Streudiagramm in der obigen Abbildung scheint zu zeigen, dass ein höherer Zeitaufwand auf der Website mit einem niedrigeren Rechnungswert korreliert. Eine weitere Modellierung kann eine genauere Beschreibung dieser Beziehung liefern. Hier kommt eine lineare Regression ins Spiel. 

LINEARE REGRESSION MIT EINER EINZIGEN VARIANTE? 

Eine lineare Regression ist ein statistisches Verfahren, bei dem die Beziehung zwischen zwei Variablen anhand eines linearen Modells als gerade Linie dargestellt wird. Wenn die Linie von links nach rechts ansteigt, ist dies ein positives Ergebnis (d. h. wenn die unabhängige Variable steigt, steigt auch die abhängige Variable). Fällt die Linie von links nach rechts, ist dies ein negatives Ergebnis (die abhängige Variable fällt, wenn die unabhängige Variable steigt). Eine mehr oder weniger flache Linie bedeutet, dass es nur eine sehr geringe Veränderung gibt. 

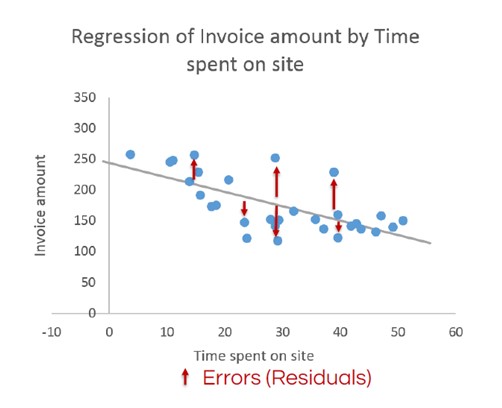
Die nachstehende Abbildung zeigt die grundlegende lineare Regression, die für das Beispiel Rechnungsbetrag vs. vor Ort verbrachte Zeit berechnet wurde. Nicht alle Datenpunkte fallen auf die entstandene Linie. Diese Datenpunkte werden als Residuen bezeichnet und werden später in diesem Artikel besprochen. Die Parameter in der Abbildung können auch als Regressionskoeffizienten bezeichnet werden. 

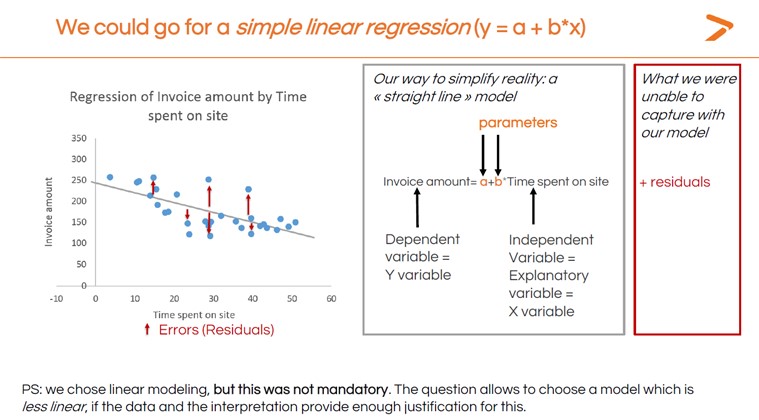
Im Folgenden werden wir Ihnen zeigen, wie Sie ein einfaches lineares Regressionsmodell in XLSTAT erstellen können.  

1. Klicken Sie auf das Icon Modellierung der Daten in der Toolbar 
2. Wählen Sie „lineare Regression“ aus dem Dropdown-Menü 
3. In der Registerkarte „Allgemein“ des erscheinenden Dialogfensters, wählen Sie die Spalte Ihres Datenblatts, die die abhängige Variable für das Feld „Y/abhängige Variablen“ darstellt 
4. Wählen Sie die Spalte in Ihrem Datenblatt, die die unabhängige Variable darstellt, für das Feld „X/abhängige Variablen“. 
5.  Klicken Sie auf „OK“. 

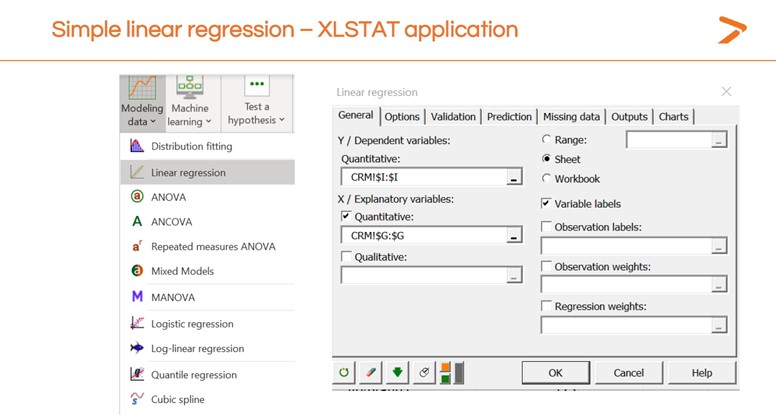
XLSTAT erstellt ein neues Blatt mit den Ergebnissen Ihrer linearen Regression, sowohl in Form eines Diagramms als auch in Form einer Datenanzeige. Nun, da Sie ein Ergebnis haben, ist es an der Zeit, dieses zu interpretieren und zu entscheiden, ob Ihr Modell nützlich ist. 

INTERPRETATION DES ERGEBNISSES: TABELLE DER MODELLPARAMETER 

Die erste Ausgabe, die Sie sich ansehen sollten, wenn Sie eine lineare Regression in XLSTAT erstellt haben, ist die Tabelle der Modellparameter. Diese zeigt den p-value (der sehr niedrig ist, was darauf hindeutet, dass die vor Ort verbrachte Zeit einen Einfluss auf die Rechnungsbeträge hat) und andere wichtige Daten. 

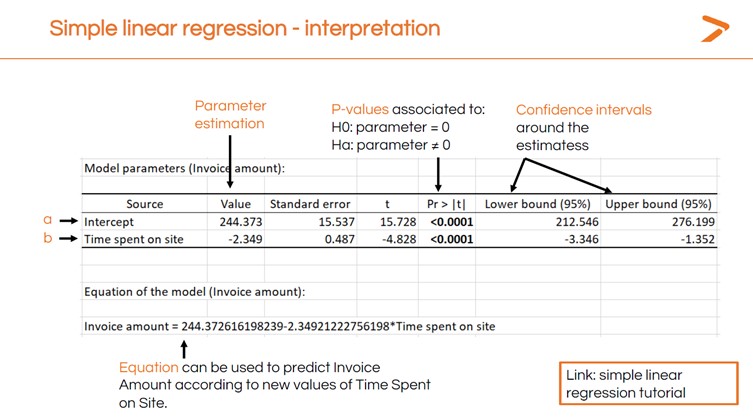
Der „Abschnittswert“ ist die Stelle auf der X-Achse, an der die lineare Regressionslinie beginnt. Dies ist der Mittelwert einer Rechnung im Datensatz. Die negative Zahl im Wert „Verweildauer“ zeigt an, dass die Regressionslinie mit einer bestimmten Rate nach unten abfällt.  

Wenn Sie nun wissen, wie lange ein Kunde auf Ihrer Website verweilt, können Sie den Rechnungswert anhand der folgenden Gleichung vorhersagen: 

244,37 - (2,349 x Verweildauer) = Rechnungswert 

Wenn also jemand 25 Minuten auf der Website verbringt, können Sie den Rechnungswert wie folgt berechnen: 

244,37 - (2,349 x 25) = 185,65 Rechnungswert 

Sie haben nun ein spezifisches Verständnis der Beziehung zwischen der auf der Website verbrachten Zeit und dem Rechnungswert, das Sie zur Vorhersage der Ergebnisse nutzen können (und zur Optimierung Ihrer Website, damit die Besucher schneller finden, was sie kaufen möchten). 

Die nächste Frage lautet: Was ist mit all diesen Residuen? Deuten sie darauf hin, dass unser Modell in irgendeiner Weise fehlerhaft ist? XLSTAT kann Ihnen helfen, Ihr Modell durch die Untersuchung der Residuen zu validieren. 

ÜBERPRÜFUNG DES MODELLS: ANNAHMEN ÜBER RESIDUEN 

Um die Gültigkeit einer linearen Regression zu bestimmen, müssen die Residuen genauer betrachtet werden. Es gibt vier Hauptannahmen, die wir über Residuen machen können, wenn ein statistisches Modell gültig ist

Wir können jeden dieser Punkte überprüfen, indem wir die folgenden Fragen stellen: 

• Sind die Residuen unabhängig, mit einer Messung pro Individuum? 
• Folgen die Residuen einer normalen glockenförmigen Verteilung? 
• Sind weniger als 5 % der Residuen Ausreißer, d. h. sie weichen in beiden Richtungen sehr weit von der Linie ab? 
• Bleibt die Varianz der Residuen entlang der Linie ungefähr gleich (Homoskedastizität)? 

Wir können auch jede dieser Annahmen mit XLSTAT überprüfen. Sie können eine schnelle grafische Diagnose Ihrer Residuen mit Hilfe der Tabelle Std. Residuen vs. Vorhersagen, die bei der Durchführung der linearen Regression erstellt wird. 

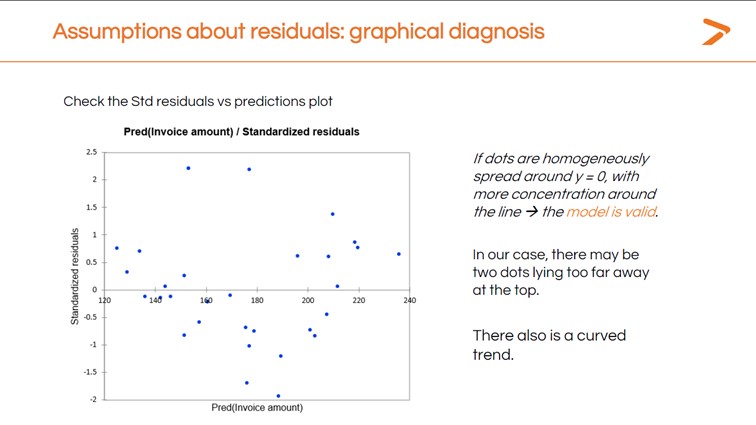
Im Idealfall würden sich die Residuen um die zentrale Linie in diesem Diagramm gruppieren. Stattdessen haben wir einen gekrümmten Trend mit mehreren Punkten, die sehr weit von der Linie entfernt sind. 

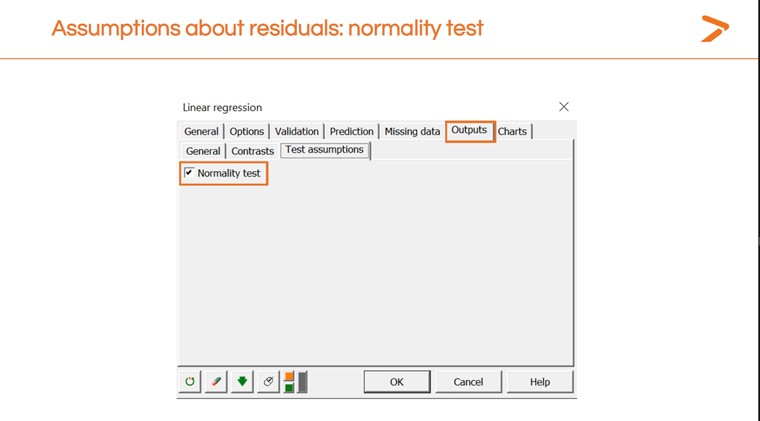
Wir können auch eine Normalitätsprüfung im Dialogfenster der linearen Regressionen in XLSTAT durchführen. 

Dies erzeugt eine weitere Ergebnistabelle mit einem p-value. Ein niedriger p-Wert bedeutet, dass das Modell gut passt; ein höherer Wert bedeutet, dass es nicht passt. Die Ergebnisse hier zeigen an, dass das Modell nicht gut angepasst ist. 

Dr. Maalouf wies darauf hin, dass Normalitätstests am besten mit größeren Datensätzen funktionieren. Kleine Datensätze werden keine zuverlässigen Ergebnisse liefern. Um zu verstehen, warum das so ist, stellen Sie sich jeden Datenpunkt wie ein Pixel auf einem Computerbildschirm vor. Wenn Sie nur ein paar Dutzend Pixel haben, können Sie nicht erkennen, was Sie da sehen. Bei Tausenden von Pixeln sehen Sie ein detaillierteres Bild. 

Hier sind zwei weitere Normalitätstestergebnisse, die häufige Muster der Verletzung illustrieren - d. h. Datenmuster in den Residuen, die darauf hinweisen, dass ein anderes Modell erforderlich sein könnte. 

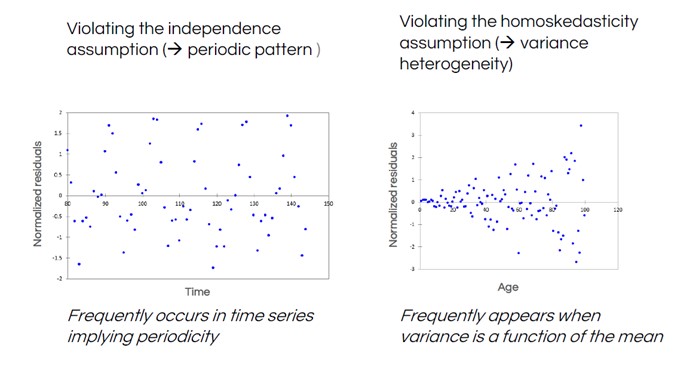
Im linken Residuen-Diagramm sehen wir eine regelmäßige „Wellenform“ in den Daten. Dies ist üblich, wenn Daten in einer Zeitreihe gemessen werden, wie z. B. Wetterdaten - die Temperaturen schwanken vorhersehbar je nach Jahreszeit, sind also nicht unabhängig. Die rechte Darstellung zeigt eine Trichterform, die anzeigt, dass der Abstand zwischen den Residuen und der Linie (die Varianz) nicht konstant ist.  

XLSTAT hilft Ihnen bei der schnellen Validierung Ihres Modells mit Tools zur Untersuchung Ihrer Residuen. Wenn Sie Probleme mit Ihren Residuen sehen, müssen Sie entscheiden, was Sie dagegen tun wollen. 

Betrachten Sie Ausreißer. Wenn es Gründe gibt, warum sie nicht im Datensatz enthalten sein sollten, können Sie sie eliminieren. 

Wenn Ihre Residuen eine eindeutige nichtlineare Beziehung aufweisen (wie die Kurve in unseren Daten aus dem Schuhgeschäft), sollten Sie einen anderen Modelltyp in Betracht ziehen. 

Entscheiden Sie, ob Sie die Daten der y-Achse mit Hilfe von Logarithmus-, Quadratwurzel- oder Box-Cox-Transformationen transformieren können (alle diese Transformationen sind in XLSTAT verfügbar). 

DURCHFÜHRUNG UND ÜBERPRÜFUNG VON MULTIPLEN LINEAREN REGRESSIONEN IN XLSTAT 

Wenn Sie untersuchen möchten, wie mehrere unabhängige Variablen Ihre abhängige Variable beeinflussen, können Sie dies auch schnell in XLSTAT tun, indem Sie eine multiple lineare Regression (MLR) durchführen. Achten Sie bei der Erstellung Ihrer MLR darauf, dass Sie nicht zu viele Variablen und Datenpunkte wählen. Das Modell, das Sie erstellen, wird wahrscheinlich „überangepasst“ sein, d.h. es ist eine sehr genaue Beschreibung Ihres Datensatzes, aber nur Ihres Datensatzes. Sie können ein überangepasstes Modell nicht für Vorhersagen verwenden, die mit

Wir werden die gleichen Schritte wie bei der einfachen linearen Regression durchführen. Lassen Sie uns zunächst eine kurze Visualisierung vornehmen.  

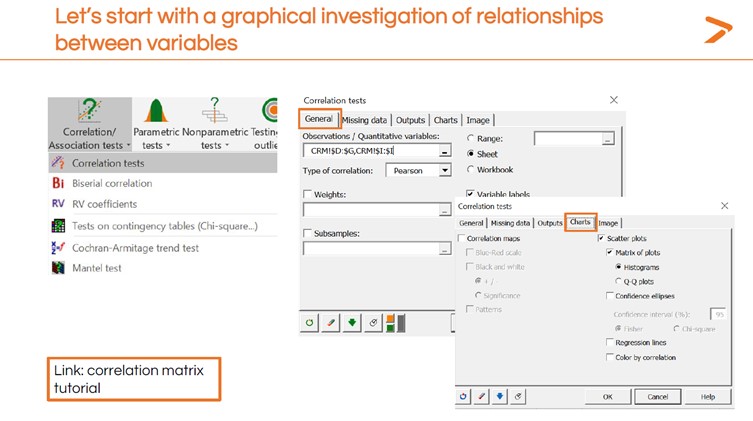
Da wir mehrere Variablen haben, wird XLSTAT mehrere Visualisierungen erstellen, um die linearen Beziehungen und Korrelationen zu untersuchen. In der untenstehenden Matrix sehen wir jede Variable im Vergleich zu jeder anderen Variable. Es gibt einige auffällige Muster. 

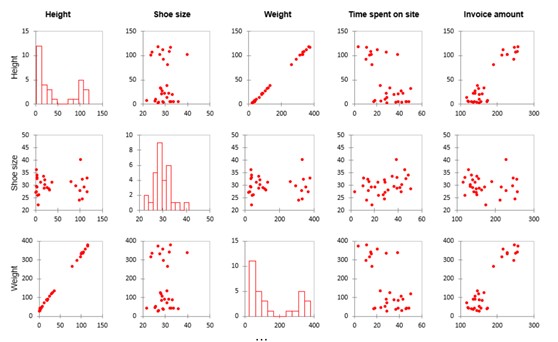
Beachten Sie die starken linienförmigen Streudiagramme in den Zeilen für Gewicht und Größe. Dies deutet darauf hin, dass diese Variablen im Wesentlichen dieselben Daten (z. B. die Größe einer Person) anzeigen. Datenpunkte, die denselben Faktor messen, werden als multikollineare Variablen bezeichnet. Sie können die eine oder andere von ihnen aus Ihrem Modell eliminieren. Wenn Sie das nicht tun, sind die Koeffizienten Ihres Modells nicht stabil und die Tests sind nicht gut. Dies wird als Multikollinearitätsproblem bezeichnet.  

Sie können auch eine Multikollinearitätsprüfung bei der Durchführung der multiplen linearen Regression in XLSTAT erstellen, indem Sie auf den Reiter „Outputs“ klicken und das Kästchen „Multikollinearitätsstatistik“ anklicken. 

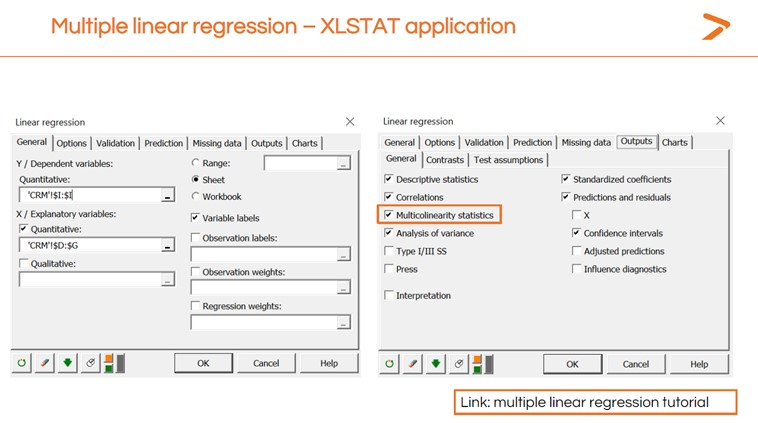
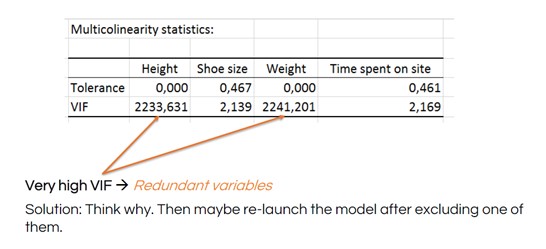
Die Multikollinearitätsstatistiken enthalten einen Varianzinflationsfaktor (VIF), um festzustellen, wie redundant eine erklärende Variable im Vergleich zu anderen ist. Eine hohe Zahl ist ein Hinweis darauf, dass Sie die redundante Variable entfernen und Ihre MLR neu starten sollten. 

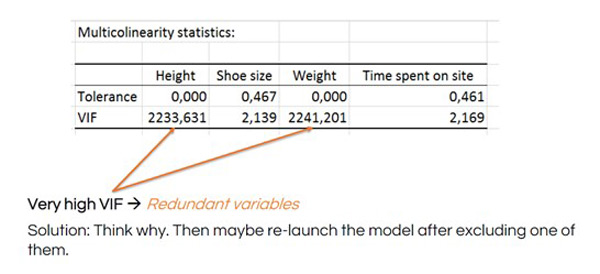
Sehen Sie, wie die VIF-Zahlen sinken, nachdem die Höhe aus der MLR entfernt wurde: 

Nachdem Sie Ihre MLR durchgeführt haben, sollten Sie die Residuen auf die gleiche Weise überprüfen wie bei der einfachen linearen Regression. In diesem Fall zeigen sich bei mehr Variablen unterschiedliche Muster in den Residuen, die auf andere statistische Modellierungstechniken hindeuten, die wir ausprobieren könnten.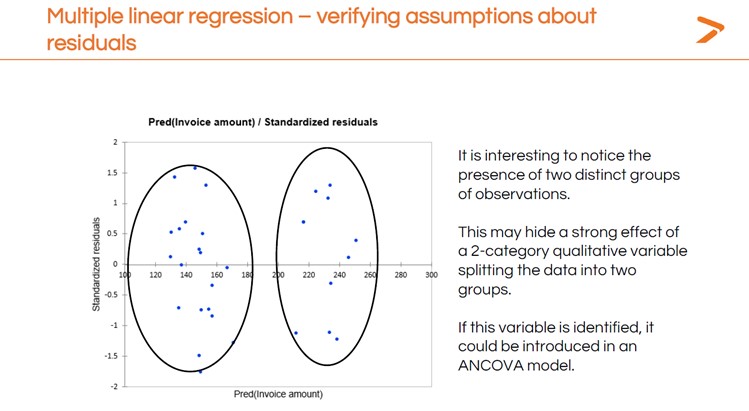 

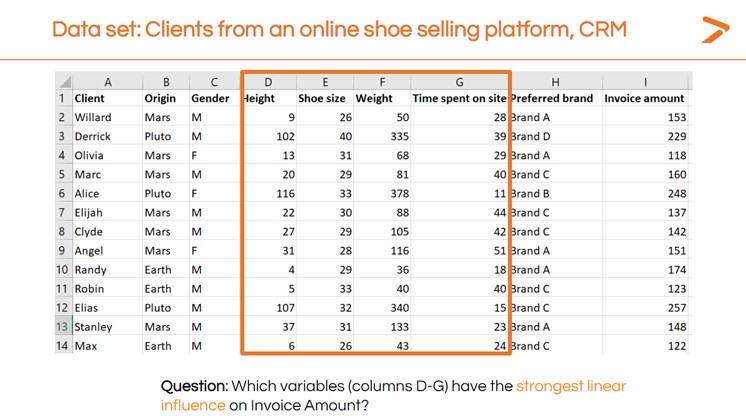
Sie werden auch die Ergebnisse der MLR interpretieren wollen, um Ihre Frage zu beantworten: Welche Variable hat den stärksten Einfluss auf den Rechnungsbetrag? 

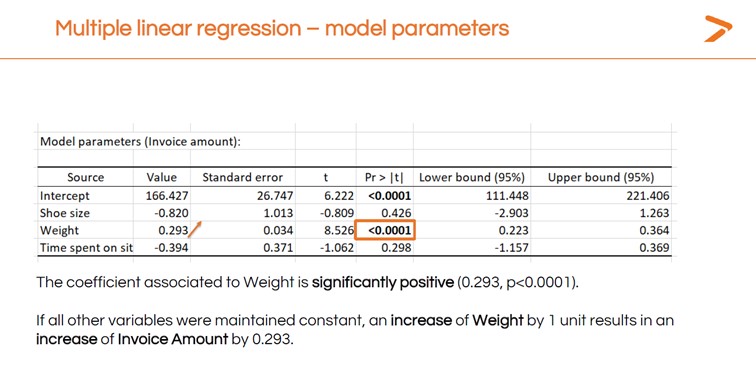
Die Ergebnisse der linearen Regressionsanalyse deuten darauf hin, dass das Gewicht die einzige Variable ist, die einen starken, signifikanten positiven Einfluss auf den Rechnungsbetrag hat, da dies die einzige Variable mit einem signifikanten Test ist. 

ERFAHREN SIE MEHR ÜBER MULTIPLE UND EINFACHE LINEARE REGRESSION MIT XLSTAT 

Sind Sie daran interessiert, mehr über die leistungsstarken statistischen Modellierungstools wie die Regressionsanalyse zu erfahren, die XLSTAT in Ihren Microsoft Excel Arbeitsbereich bringt? Fordern Sie noch heute eine kostenlose Demo an. Sie können auch den XLSTAT YouTube Kanal besuchen, um weitere Tutorial-Videos zu sehen.