Regressionsanalyse: Die Methode auf die Daten abstimmen

Was ist die Regressionsanalyse?

Die Regressionsanalyse ist einer der Eckpfeiler der statistischen Methoden, die bei der Datenanalyse und Vorhersagemodellierung eingesetzt werden. Es handelt sich dabei um eine leistungsstarke statistische Technik, mit der die Beziehung zwischen Variablen untersucht werden kann, was sie zu einem unverzichtbaren Werkzeug in Bereichen wie Wirtschaft, Biologie, Sozialwissenschaften und anderen macht.

Das Hauptziel der Regressionsanalyse besteht darin, festzustellen, wie sich Änderungen der unabhängigen Variablen auf die abhängige Variable auswirken. Dies hilft, die den Daten zugrunde liegenden Mechanismen besser zu verstehen, um bessere Vorhersagen und Entscheidungen treffen zu können.

Welche verschiedenen Arten der Regressionsanalyse gibt es?

Die Vielseitigkeit von Regressionsmodellen ermöglicht ihre Anwendung auf eine Vielzahl von Datentypen und Forschungsszenarien. Die verschiedenen Arten von Regressionsmodellen eignen sich jedoch speziell für unterschiedliche Datentypen und Beziehungen, so dass es wichtig ist, je nach Art der Daten und den Forschungszielen das richtige Modell auszuwählen.

Unabhängig davon, ob es sich um kontinuierliche, kategoriale, binäre oder zählungsbasierte Daten handelt, ist jede Art von Regressionsmethode so konzipiert, dass sie den Forschungszielen und einzigartigen Eigenschaften des Datensatzes gerecht wird. Während die lineare Regression beispielsweise ideal für die Modellierung einfacher Beziehungen bei kontinuierlichen Variablen ist, eignet sich die logistische Regression besser für binäre oder kategoriale Ergebnisse. Ebenso können bei der Arbeit mit komplexen, hochdimensionalen Daten fortgeschrittenere Techniken wie Partial Least Squares (PLS)-Regression, Ridge- und Lasso-Regression erforderlich sein.

Welches Regressionsmodell ist das richtige für Ihre Datenanalyse?

Die Wahl des falschen Regressionsmodells kann zu ungenauen Schlussfolgerungen und schlechter Vorhersageleistung führen. Um das richtige Modell für Ihre Daten zu bestimmen, müssen Sie die Stärken, Schwächen und geeigneten Anwendungen der einzelnen Regressionsmodelltypen kennen.

In diesem Leitfaden zur Regressionsanalyse besprechen wir mehrere gängige Regressionstypen, heben die Datentypen hervor, für die sie am besten geeignet sind, und illustrieren ihre praktischen Anwendungen in verschiedenen Branchen.

Laden Sie Ihre kostenlose Testversion von XLSTAT herunter und beginnen Sie mit der Anwendung dieser Regressionsmodelle auf Ihre Daten.

1. Lineare Regression

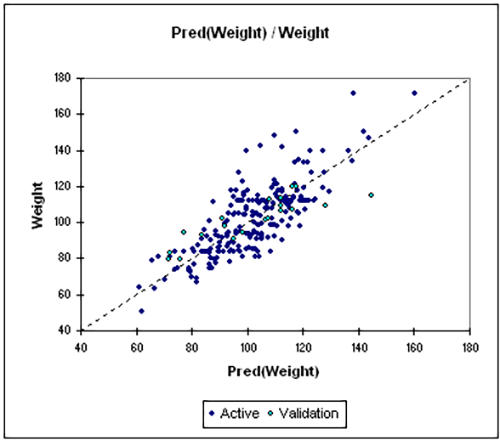
• Datentyp: Kontinuierliche abhängige Variable mit einer oder mehreren kontinuierlichen unabhängigen Variablen.
• Beschreibung: Die lineare Regression (einschließlich einfacher linearer Regression und multipler linearer Regression) untersucht die Beziehung zwischen einer abhängigen Variablen und einer oder mehreren unabhängigen Variablen. Sie setzt eine lineare Beziehung voraus und wird verwendet, wenn sowohl das Ergebnis als auch die Prädiktoren kontinuierlich sind. Ziel ist es, die abhängige Variable mit Hilfe der Prädiktoren vorherzusagen oder zu erklären. Dieses Modell hilft bei der Analyse der kombinierten Wirkung mehrerer Faktoren auf das Ergebnis.
• Beispiel: Schätzung des Einflusses von Einkommen und Alter auf die Ausgabengewohnheiten.

Erfahren Sie mehr über die lineare Regressionsanalyse >>

2. Logistische Regression

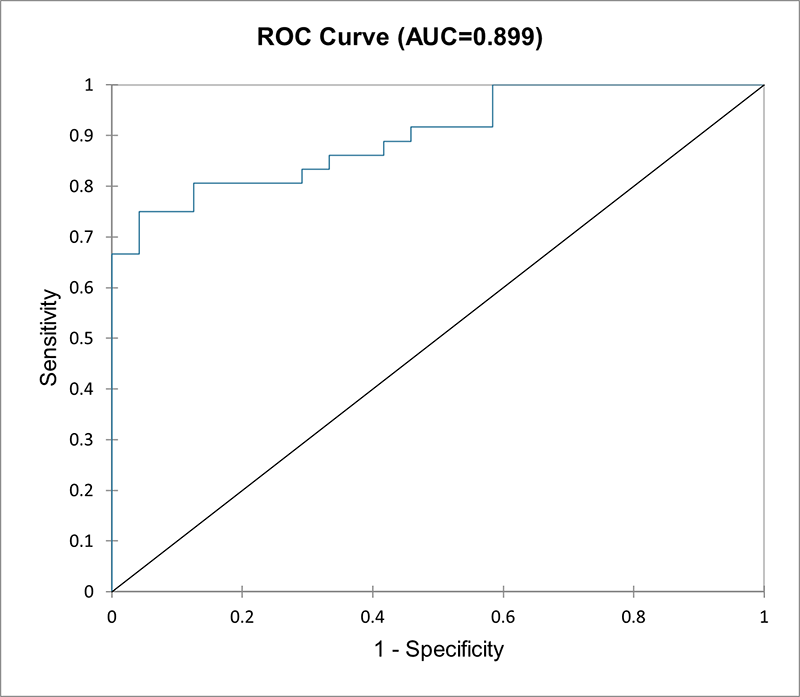
• Datentyp: Binäre oder kategoriale abhängige Variable (0 oder 1). Die multinomiale logistische Regression ist ebenfalls möglich, wenn die abhängige Variable mehr als 2 Kategorien hat. Kontinuierliche oder kategoriale unabhängige Variablen.
• Beschreibung: Die logistische Regression wird verwendet, wenn die abhängige Variable kategorisch ist (z. B. Erfolg/Misserfolg, ja/nein, klein/mittel/groß). Die Ausgabe wird mithilfe einer logistischen Funktion modelliert, die Wahrscheinlichkeiten für verschiedene Ergebnisse vorhersagt.
• Beispiel: Vorhersage, ob ein Kunde ein Produkt kaufen wird (ja/nein), basierend auf Einkommen, Alter und bisherigem Kaufverhalten.

Erfahren Sie mehr über logistische Regression >>

3. Partielle kleinste Quadrate (PLS) Regression

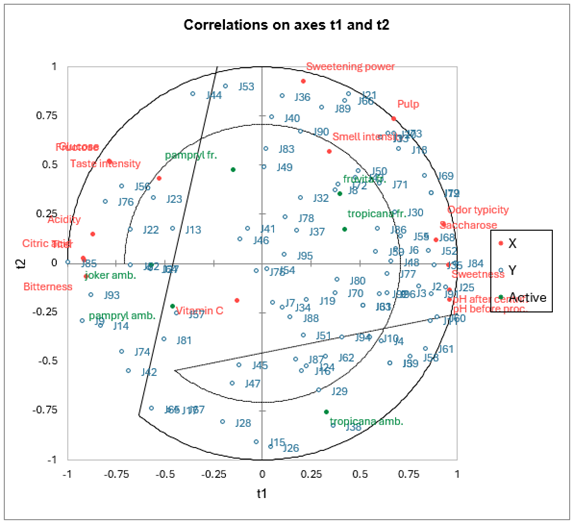
• Datentyp: Multivariate Daten mit hochdimensionalen Prädiktoren (kollinear und verrauscht). Kontinuierliche oder kategoriale unabhängige Variablen.
• Beschreibung: Die PLS-Regression ist besonders nützlich, wenn die Prädiktorvariablen hochgradig kollinear sind (d. h., sie sind stark miteinander korreliert) oder wenn die Anzahl der Prädiktoren die Anzahl der Beobachtungen übersteigt. PLS kombiniert Merkmale der Hauptkomponentenanalyse (PCA) und der multiplen Regression, indem die Prädiktoren in einen neuen Raum projiziert werden und eine lineare Beziehung zwischen diesen Projektionen und der abhängigen Variable gefunden wird.
• Anwendung: PLS wird häufig in der Chemometrie, der Bioinformatik und anderen Bereichen eingesetzt, die mit hochdimensionalen Datensätzen arbeiten.
• Beispiel: Vorhersage der chemischen Eigenschaften einer Verbindung auf der Grundlage einer großen Menge spektroskopischer Messungen.

Erfahren Sie mehr über Partial Least Squares Regression >>

4. Ridge-, Lasso- und elastische Netzregression

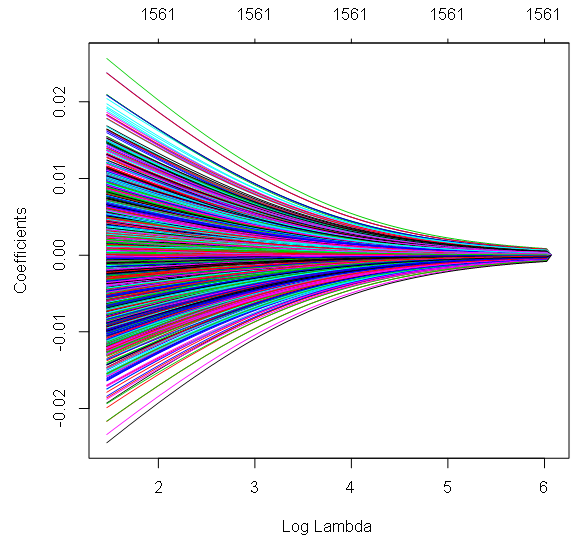
• Datentyp: Kontinuierliche abhängige Variable mit vielen Prädiktorvariablen (möglicherweise korreliert). Kontinuierliche oder kategoriale unabhängige Variablen.
• Beschreibung: Hierbei handelt es sich um Regularisierungsverfahren, die die Verlustfunktion modifizieren, um eine Überanpassung zu verhindern, insbesondere bei Multikollinearität. Bei der Ridge-Regression wird die Summe der quadrierten Koeffizienten bestraft, während bei der Lasso-Regression der absolute Wert der Koeffizienten bestraft wird, wodurch häufig einige Koeffizienten auf Null gesetzt werden. Elastic Net ist eine Mischung aus diesen beiden Methoden.
• Beispiel: Die Ridge-Regression wird häufig in der Genomik zur Vorhersage von Krankheitsrisiken auf der Grundlage von Tausenden von genetischen Markern verwendet.

Erfahren Sie mehr über Ridge-Regression >>

Erfahren Sie mehr über die Lasso-Regression >>

5. Log-lineare (oder Poisson-) Regression

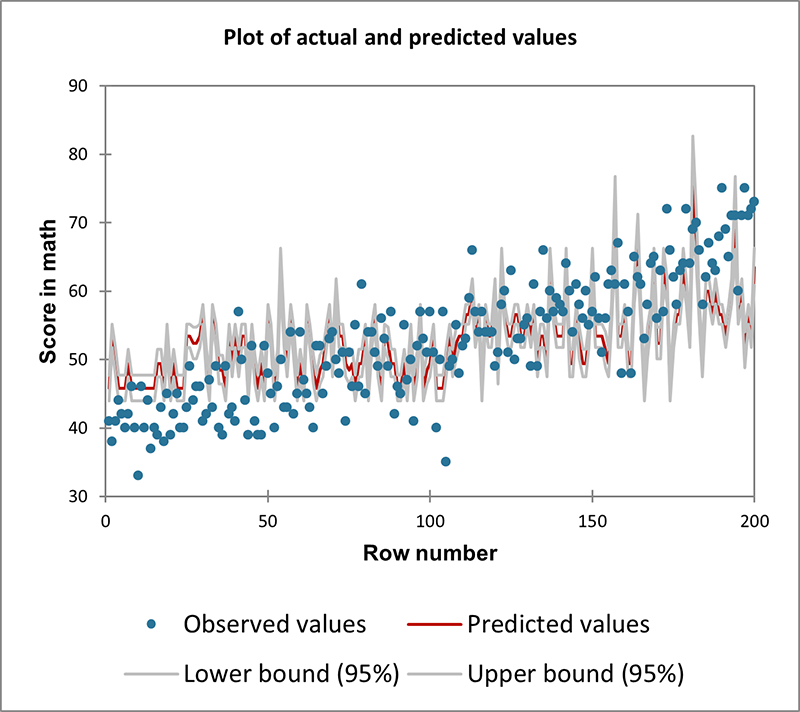
• Datentyp: Zähldaten (Anzahl der Vorkommnisse eines Ereignisses). Kontinuierliche oder kategoriale unabhängige Variablen.
• Beschreibung: Die Poisson-Regression ist ideal für die Modellierung von Zähldaten und Raten, insbesondere wenn das Ergebnis die Anzahl des Auftretens eines Ereignisses in einem festen Intervall (z.B. Zeit, Entfernung) darstellt.
• Beispiel: Modellierung der Anzahl der in einem Callcenter eingegangenen Anrufe in Abhängigkeit von der Tageszeit und der Anzahl der diensthabenden Mitarbeiter.

Erfahren Sie mehr über log-lineare Regression >>

6. Quantile Regression

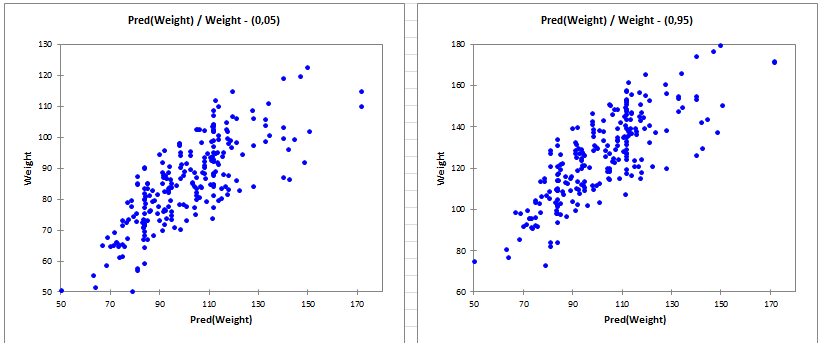
• Datentyp: Kontinuierliche abhängige Variable mit heterogenen Beziehungen zwischen den Quantilen.
• Beschreibung: Im Gegensatz zur linearen Regression, die den Mittelwert der abhängigen Variable in Abhängigkeit von den Prädiktoren schätzt, schätzt die Quantilsregression den bedingten Median oder andere Quantile der abhängigen Variable. Dies macht sie nützlich, wenn die Beziehung zwischen den Variablen an verschiedenen Punkten der Verteilung variiert und nicht über den gesamten Datensatz konstant ist.
• Anwendung: Die Quantilsregression ist besonders effektiv, wenn die Daten eine nicht konstante Varianz aufweisen oder wenn Ausreißer bestimmte Teile der Verteilung beeinflussen.
• Beispiel: Untersuchung der Auswirkungen von Bildung auf verschiedene Quantile der Einkommensverteilung, wobei Faktoren das untere, mittlere und obere Segment unterschiedlich beeinflussen können.

Erfahren Sie mehr über die Quantilsregression >>

7. Nichtparametrische Regression (Kernel und Lowess)

• Datentyp: Komplexe Daten ohne eine vordefinierte funktionale Beziehung zwischen den Variablen.
• Beschreibung: Die nichtparametrische Regression geht nicht von einer bestimmten funktionalen Form für die Beziehung zwischen unabhängigen und abhängigen Variablen aus. Stattdessen erlaubt sie den Daten, die Form der Beziehung zu bestimmen. Polynomielle Regressionen werden häufig in nichtparametrischen Methoden verwendet.
• Anwendung: Diese Methoden sind nützlich, wenn es wenig Vorwissen über die funktionale Form der Beziehung zwischen den Variablen gibt oder wenn die Daten sehr flexibel oder komplex sind.
• Beispiel: Modellierung der Beziehung zwischen Temperatur und Pflanzenwachstum, wobei die Beziehung über verschiedene Temperaturbereiche hinweg nichtlinear variieren kann.

Erfahren Sie mehr über die nichtparametrische Regression >>

8. Nichtlineare Regression

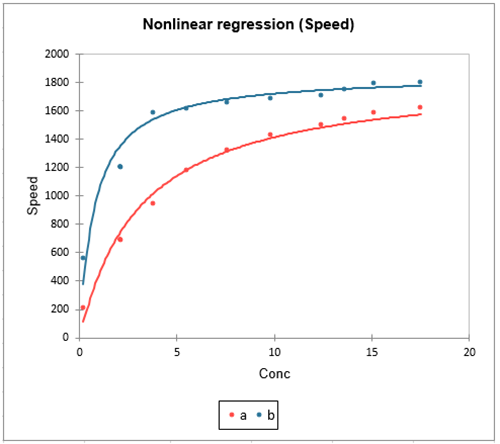
• Datentyp: Kontinuierliche abhängige Variable mit einer nichtlinearen Beziehung zwischen den Variablen.
• Beschreibung: Die nichtlineare Regression wird verwendet, wenn die Beziehung zwischen abhängigen und unabhängigen Variablen nicht angemessen durch eine lineare Gleichung erfasst werden kann. Das Modell kann verschiedene Formen annehmen, wie z. B. exponentielle, logarithmische oder polynomiale Beziehungen. Die nichtlineare Regression erfordert iterative Methoden zur Parameterschätzung, da die Parameter oft nicht explizit gelöst werden können.
• Anwendung: Sie wird häufig in Bereichen wie Biologie, Wirtschaft und Technik angewandt, in denen Beziehungen von Natur aus nicht linear sind.
• Beispiel: Modellierung des Bevölkerungswachstums im Laufe der Zeit anhand einer logistischen Wachstumskurve, bei der sich das Wachstum zunächst beschleunigt, sich aber verlangsamt, wenn die Bevölkerung die Tragfähigkeit der Umwelt erreicht.

Erfahren Sie mehr über die nichtlineare Regression >>

Lassen Sie die Regressionsanalyse für sich arbeiten

Die Auswahl der besten Regressionsanalyse muss nicht entmutigend sein. Mit den richtigen Tools können Sie diese Methoden leicht erforschen und auf Ihre Daten anwenden, ohne dass Sie ein umfangreiches statistisches Hintergrundwissen benötigen. Um Ihnen den Einstieg zu erleichtern, bieten wir Ihnen eine kostenlose 14-tägige Testversion von XLSTAT an - einer leistungsstarken und dennoch benutzerfreundlichen Statistiksoftware, die Ihnen helfen kann, tiefere Einblicke zu gewinnen und die Zuverlässigkeit Ihrer Forschungs- und Geschäftsentscheidungen zu verbessern.

Downloaden Sie die kostenlose XLSTAT Testversion