Cochran-Armitage trend test

When to use a Cochran-Armitage trend test

The Cochran Armitage trend is used to test if a series of proportions, possibly computed from a contingency table, can be considered as varying linearly with an ordinal or continuous variable.

It can be a one- or two-sided test.

What is the Cochran-Armitage trend test

The Cochran-Armitage test allows to test if a series of proportions, can be considered as varying linearly with an ordinal or continuous score variable.

If X is the score variable, the statistic that is computed to test for the linearity is given by:

z = [Ʃ_i=1..r n_r1(X_i - X)] / √ p₊₁ (1– p₊₁) s²

with s²=Ʃ_i=1..r n_i+(X_i - X)²

Note: if X is an ordinal variable, the minimum value of X has no influence on the value of z.

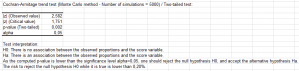
In the case of the two-tailed (or two-sided) test, the null (H₀) and alternative (H_a) hypotheses are:

• H₀: z  = 0
• H_a: z ≠ 0

Note: z is asymptotically distributed as a standard Normal variable. Some statistical programs use z² to test the linearity. z² follows a Chi-square distribution with one degree of freedom.

In the one-tailed case, you need to distinguish the left-tailed (or lower-tailed or lower one-sided) test and the right-tailed (or upper-tailed or upper one-sided) test. In the left-tailed test, the following hypotheses are used:

• H₀: z  = 0
• H_a: z < 0

If H_a is chosen, one concludes that the proportions decrease when the score variable increases.

In the right-tailed test, the following hypotheses are used:

• H₀: z  = 0
• H_a: z > 0

If H_a is chosen, one concludes that the proportions increase when the score variable increases.