Análisis de regresión: Adecuación del método a los datos

¿Qué es el análisis de regresión?

El análisis de regresión es una de las piedras angulares de los métodos estadísticos utilizados en el análisis de datos y la elaboración de modelos predictivos. Se trata de una potente técnica estadística diseñada para examinar la relación entre variables, lo que la convierte en una herramienta esencial en campos como la economía, la biología y las ciencias sociales, entre otros.

El objetivo principal del análisis de regresión es determinar cómo los cambios en las variables independientes influyen en la variable dependiente, lo que ayuda a comprender mejor los mecanismos subyacentes que impulsan los datos para hacer mejores predicciones y tomar mejores decisiones.

¿Cuáles son los distintos tipos de análisis de regresión?

La versatilidad de los modelos de regresión permite aplicarlos a una amplia gama de tipos de datos y escenarios de investigación. Sin embargo, los distintos tipos de modelos de regresión están especialmente indicados para tratar distintos tipos de datos y relaciones, por lo que es esencial elegir el adecuado en función de la naturaleza de los datos y los objetivos de la investigación.

Independientemente de que los datos sean continuos, categóricos, binarios o de recuento, cada tipo de método de regresión está diseñado para adaptarse a los objetivos de la investigación y a las cualidades únicas del conjunto de datos. Por ejemplo, mientras que la regresión lineal es ideal para modelar relaciones directas en variables continuas, la regresión logística es más adecuada para resultados binarios o categóricos. Del mismo modo, cuando se trabaja con datos complejos y de alta dimensión, pueden ser necesarias técnicas más avanzadas como la regresión por mínimos cuadrados parciales (PLS), la regresión Ridge y la regresión Lasso.

¿Qué modelo de regresión es el adecuado para su análisis de datos?

La elección de un modelo de regresión incorrecto puede dar lugar a conclusiones inexactas y a un rendimiento predictivo deficiente. Para determinar el modelo adecuado para sus datos, debe comprender los puntos fuertes, los puntos débiles y las aplicaciones apropiadas de cada tipo de modelo de regresión.

En esta guía de análisis de regresión, discutiremos varios tipos comunes de regresión, destacaremos los tipos de datos para los que son más adecuados e ilustraremos sus aplicaciones prácticas en varias industrias.

Descargue su versión de prueba gratuita de XLSTAT para empezar a aplicar estos modelos de regresión a sus datos.

1. Regresión lineal

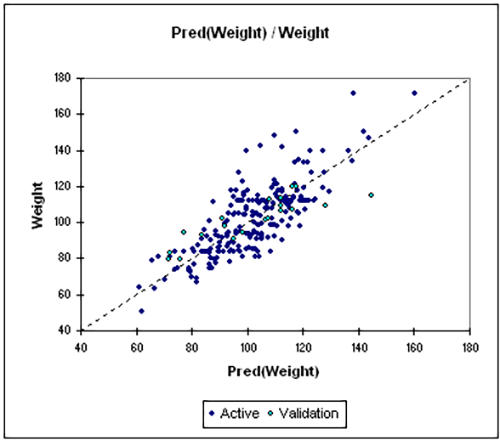
• Tipo de datos: Variable dependiente continua con una o más variables independientes continuas.
• Descripción: La regresión lineal (que incluye tanto la regresión lineal simple como la regresión lineal múltiple) examina la relación entre una variable dependiente y una o más variables independientes. Supone una relación lineal y se utiliza cuando tanto el resultado como los predictores son continuos. El objetivo es predecir o explicar la variable dependiente utilizando los predictores. Este modelo ayuda a analizar el efecto combinado de múltiples factores sobre el resultado.
• Ejemplo: Estimación de la influencia de los ingresos y la edad en los hábitos de gasto.

Más información sobre el análisis de regresión lineal >>

2. Regresión logística

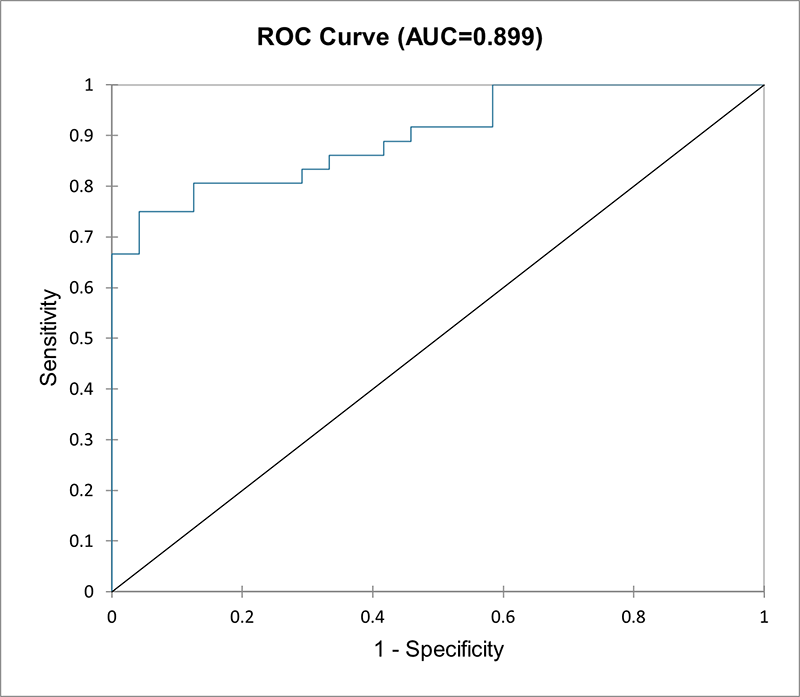
• Tipo de datos: Variable dependiente binaria o categórica (0 o 1). La regresión logística multinomial también es posible si la variable dependiente tiene más de 2 categorías. Variables independientes continuas o categóricas.
• Descripción: La regresión logística se utiliza cuando la variable dependiente es categórica (por ejemplo, éxito/fracaso, sí/no, pequeño/mediano/alto). La salida se modela utilizando una función logística que predice probabilidades de diferentes resultados.
• Ejemplo: Predecir si un cliente comprará un producto (sí/no) en función de sus ingresos, edad y comportamiento de compra anterior.

Más información sobre regresión logística >>

3. Regresión por mínimos cuadrados parciales (PLS)

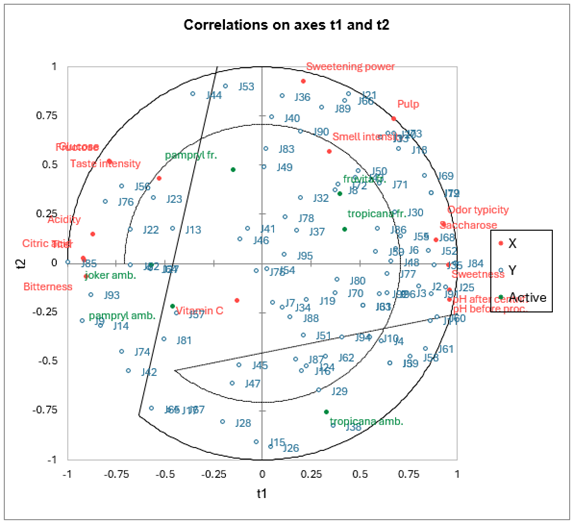
• Tipo de datos: Datos multivariantes con predictores de alta dimensión (colineales y ruidosos). Variables independientes continuas o categóricas.
• Descripción: La regresión PLS es particularmente útil cuando las variables predictoras son altamente colineales (es decir, están fuertemente correlacionadas entre sí) o cuando el número de predictores supera el número de observaciones. PLS combina características del análisis de componentes principales (ACP) y de la regresión múltiple proyectando los predictores en un nuevo espacio y encontrando una relación lineal entre estas proyecciones y la variable dependiente.
• Aplicación: El PLS se utiliza ampliamente en quimiometría, bioinformática y otros campos relacionados con conjuntos de datos de alta dimensión.
• Ejemplo: Predicción de las propiedades químicas de un compuesto a partir de un gran conjunto de mediciones espectroscópicas.

Más información sobre la regresión por mínimos cuadrados parciales >>

4. Regresión Ridge, Lasso y de red elástica

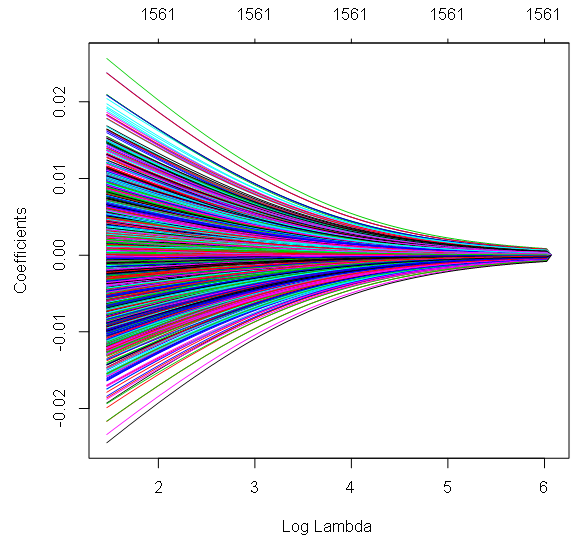
• Tipo de datos: Variable dependiente continua con muchas variables predictoras (posiblemente correlacionadas). Variables independientes continuas o categóricas.
• Descripción: Se trata de técnicas de regularización que modifican la función de pérdida para evitar el sobreajuste, especialmente cuando se trata de multicolinealidad. La regresión Ridge penaliza la suma de los coeficientes al cuadrado, mientras que la regresión Lasso penaliza el valor absoluto de los coeficientes, a menudo llevando algunos coeficientes a cero. La red elástica es una mezcla de estos dos métodos.
• Ejemplo: La regresión Ridge se utiliza a menudo en genómica para predecir el riesgo de enfermedad a partir de miles de marcadores genéticos.

Más información sobre la regresión Ridge >>

Más información sobre la regresión Lasso >>

5. Regresión logarítmica lineal (o de Poisson)

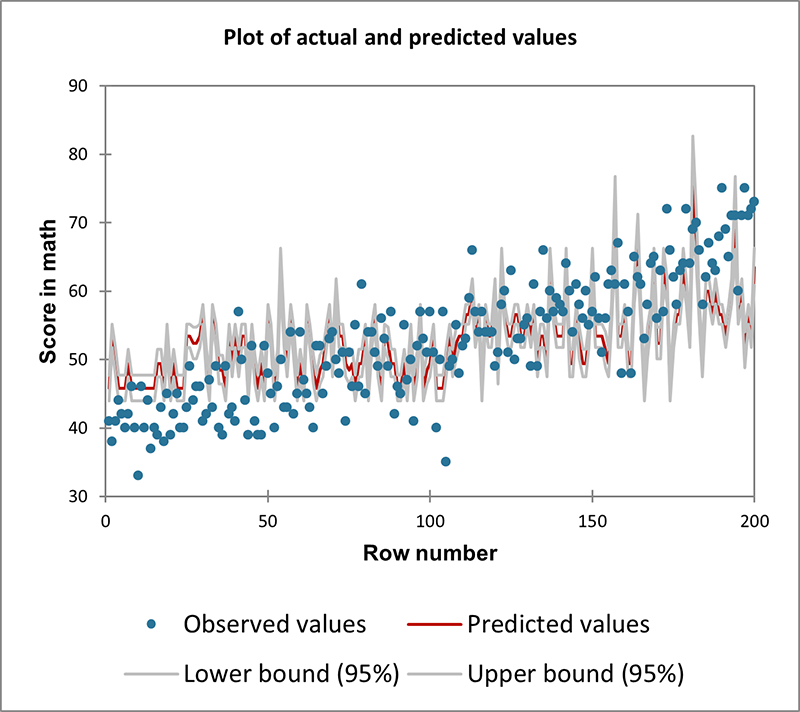
• Tipo de datos: Datos de recuento (número de ocurrencias de un evento). Variables independientes continuas o categóricas.
• Descripción: La regresión de Poisson es ideal para modelar datos de recuento y tasas, especialmente cuando el resultado representa el número de veces que ocurre un evento en un intervalo fijo (por ejemplo, tiempo, distancia).
• Ejemplo: Modelización del número de llamadas recibidas en un centro de llamadas en función de la hora del día y el número de operadores de guardia.

Más información sobre regresión log-lineal >>

6. Regresión cuantil

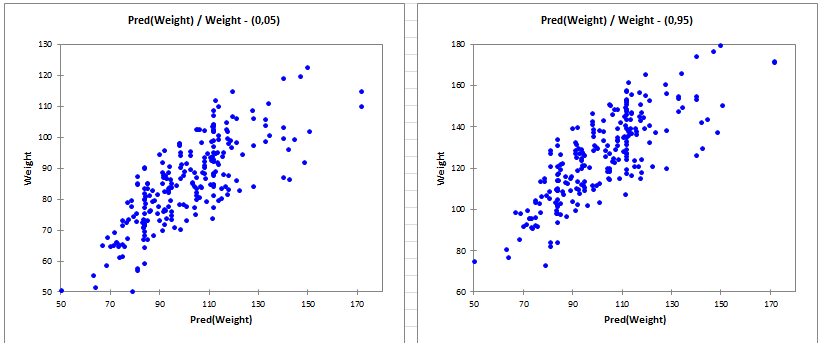
• Tipo de datos: Variable dependiente continua con relaciones heterogéneas entre cuantiles.
• Descripción: A diferencia de la regresión lineal, que estima la media de la variable dependiente condicionada a los predictores, la regresión cuantil estima la mediana condicional u otros cuantiles de la variable dependiente. Esto la hace útil cuando la relación entre las variables varía en diferentes puntos de la distribución, en lugar de ser constante en todo el conjunto de datos.
• Aplicación: La regresión cuantil es especialmente eficaz cuando los datos presentan una varianza no constante o cuando los valores atípicos influyen en partes específicas de la distribución.
• Ejemplo: Estudiar el impacto de la educación en diferentes cuantiles de la distribución de la renta, donde los factores pueden influir de forma diferente en los segmentos inferior, medio y superior.

Más información sobre regresión cuantil >>

7. Regresión no paramétrica (Kernel y Lowess)

• Tipo de datos: Datos complejos sin una relación funcional predefinida entre variables.
• Descripción: La regresión no paramétrica no asume una forma funcional específica para la relación entre las variables independientes y dependientes. En su lugar, permite que los datos determinen la forma de la relación La regresión polinómica se utiliza habitualmente en los métodos no paramétricos.
• Aplicación: Estos métodos son útiles cuando hay poco conocimiento previo sobre la forma funcional de la relación entre variables o cuando los datos son muy flexibles o complejos.
• Ejemplo: Modelización de la relación entre la temperatura y el crecimiento de las plantas cuando la relación puede variar de forma no lineal en diferentes rangos de temperatura.

Más información sobre regresión no paramétrica >>

8. Regresión no lineal

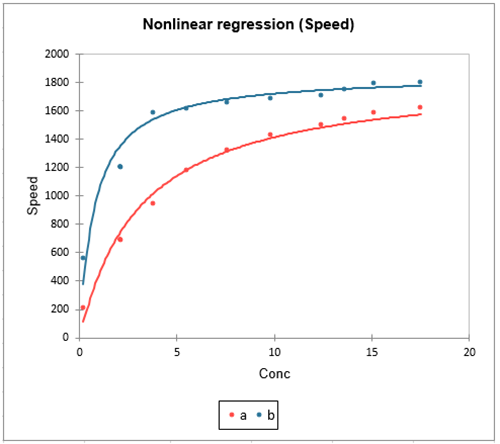
• Tipo de datos: Variable dependiente continua con una relación no lineal entre variables.
• Descripción: La regresión no lineal se utiliza cuando la relación entre las variables dependientes e independientes no puede ser adecuadamente capturada por una ecuación lineal. El modelo puede adoptar diversas formas, como relaciones exponenciales, logarítmicas o polinómicas. La regresión no lineal requiere métodos iterativos para la estimación de los parámetros, ya que a menudo éstos no pueden resolverse explícitamente.
• Aplicación: Suele aplicarse en campos como la biología, la economía y la ingeniería, donde las relaciones son intrínsecamente no lineales.
• Ejemplo: Modelización del crecimiento de la población a lo largo del tiempo mediante una curva de crecimiento logística, en la que el crecimiento se acelera al principio pero se ralentiza cuando la población alcanza la capacidad de carga del entorno.

Más información sobre Regresión no lineal >>

Empiece a hacer que el análisis de regresión trabaje para usted

Elegir el mejor análisis de regresión no tiene por qué ser desalentador. Con las herramientas adecuadas, puede explorar y aplicar fácilmente estos métodos a sus datos sin necesidad de tener una amplia formación estadística. Para ayudarle a empezar, le ofrecemos una versión de prueba gratuita de 14 días de XLSTAT, un software estadístico potente y fácil de usar que puede ayudarle a obtener información más profunda y mejorar la fiabilidad de sus investigaciones y decisiones empresariales.

Descargar prueba gratuita de XLSTAT