Cómo crear y validar regresiones lineales múltiples y simples en XLSTAT

Si usted es como la mayoría de los investigadores y analistas de datos, probablemente se encuentre en situaciones en las que necesite predecir tendencias futuras, identificar los factores clave que influyen en un resultado o simplemente comprender la conexión entre variables. En estos casos, la regresión lineal es una herramienta fundamental para cualquiera que intente comprender las relaciones dentro de sus datos y hacer predicciones basadas en esos conocimientos. Sin embargo, iniciarse en la regresión lineal puede resultar desalentador, especialmente para los principiantes en el análisis estadístico. 

Aquí es donde las herramientas de análisis estadístico fáciles de usar, como XLSTAT, y una formación exhaustiva se convierten en esenciales, salvando las distancias entre la necesidad de métodos estadísticos avanzados y la facilidad para aplicarlos eficazmente. 

En uno de nuestros seminarios web, Jean-Paul Maalouf, consultor de ciencia de datos, explicó a los asistentes cómo y por qué utilizar un modelo de regresión lineal, al tiempo que demostró cómo XLSTAT puede ayudar a detectar errores comunes en este tipo de modelización.  

Vea el webinar o siga leyendo para aprender a crear y validar regresiones lineales múltiples y simples en XLSTAT con el Dr. Maalouf. 

ACERCA DEL SOFTWARE ESTADÍSTICO XLSTAT 

Como vamos a discutir cómo utilizar XLSTAT para su modelado de regresión lineal, puede ser útil familiarizarse con la funcionalidad general de este potente software estadístico. XLSTAT puede ayudar a potenciar y agilizar su análisis estadístico, todo ello dentro de Microsoft Excel. XLSTAT pone a su alcance más de 300 funciones para analizar, modelar y visualizar datos, y estas funciones se dividen en diferentes categorías de herramientas: 

• Descriptivas - Explican variables individuales o vínculos entre dos variables (por ejemplo, encontrar la media o la desviación estándar en un conjunto de datos).
• Exploratoria: búsqueda de patrones en grandes conjuntos de datos.  
• Pruebas estadísticas: análisis de datos para demostrar o refutar una hipótesis. 
• Modelización estadística - Comprender cómo se comporta una variable bajo la influencia de otras variables y, a continuación, utilizar esa relación, a menudo expresada mediante una ecuación de regresión, para hacer predicciones. 
• Preparación de datos: proceso por el que se preparan los datos brutos para su análisis. 
• Visualización de datos: utilización de gráficos y diagramas para representar la información de los datos. 
• Aprendizaje automático - Aprovechamiento de la IA para aprender de los datos y predecir resultados. 

Además, XLSTAT contiene funciones avanzadas específicas para los campos de los sensores, la investigación de mercados, las ciencias de la vida y la calidad.  

En este artículo, nos centraremos en las pruebas estadísticas y el modelado estadístico. Para obtener más información sobre estas otras funciones de XLSTAT, consulte nuestros tutoriales. 

¿QUÉ SON LOS MODELOS ESTADÍSTICOS Y LAS PRUEBAS ESTADÍSTICAS? 

Para empezar por el principio, un modelo estadístico es una representación simplificada de la realidad a partir de datos, que a menudo implica un análisis de regresión para establecer relaciones lineales. Con el modelado estadístico, podemos entender cómo se comporta una variable cuando cambian otras variables. Una vez que tenemos un modelo estadístico cuya precisión y utilidad se han verificado, podemos utilizarlo para hacer predicciones sobre los resultados utilizando nuevos datos. 

Las pruebas estadísticas son el proceso de utilizar modelos estadísticos para demostrar o refutar una hipótesis. En términos más generales, las pruebas estadísticas tratan de determinar si la variable A cambia significativamente cuando se ve afectada por la variable B. Esto conduce a dos resultados posibles: 

• La hipótesis nula: No hay ningún cambio significativo de la variable A en relación con la variable B. 
• La hipótesis alternativa: Hay un cambio significativo de la variable A en relación con la variable B. 

Las pruebas estadísticas dan como resultado un número denominado valor de probabilidad, o valor p. El valor p expresa la probabilidad de que la hipótesis nula sea cierta, es decir, la probabilidad de que no haya cambios significativos. El valor p es un número comprendido entre 0 y 1: cuanto más se acerque a 1, menos significativo será el resultado. Cada prueba estadística requiere que los investigadores establezcan su propio umbral de valor p. 

¿CÓMO ELEGIR UN MÉTODO DE MODELIZACIÓN ESTADÍSTICA PARA MIS DATOS? 

Existen muchísimos tipos diferentes de modelos estadísticos. El método que elija dependerá de los datos que tenga y de lo que quiera entender de ellos. El Dr. Maalouf explicó algunos de los métodos de modelización más comunes para distintos tipos de variables. 

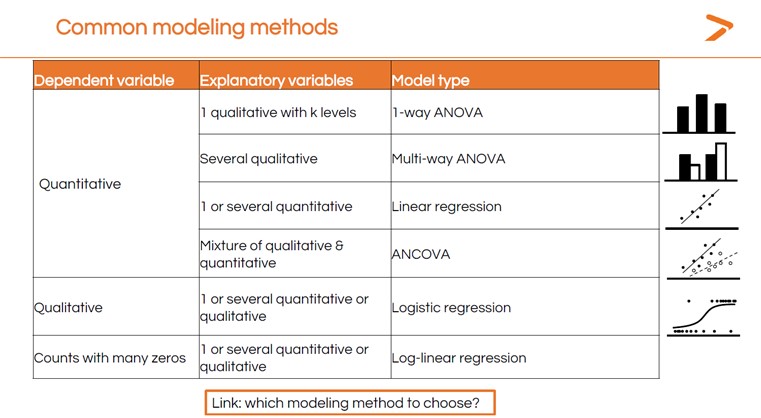
Con tantas opciones, puede resultar difícil elegir la prueba estadística correcta para su análisis. Ahí es donde la herramienta MyAssistant de XLSTAT puede ayudarle. Simplemente responda a una secuencia de preguntas, y MyAssistant le dirigirá a la prueba adecuada para su análisis de datos. También ofrecemos una breve guía de modelización estadística que puede ayudarle a elegir qué método de modelización utilizar en XLSTAT en función de sus datos y del objetivo de su análisis.  

¿CÓMO DETERMINAR QUÉ VARIABLES SON DEPENDIENTES O INDEPENDIENTES? 

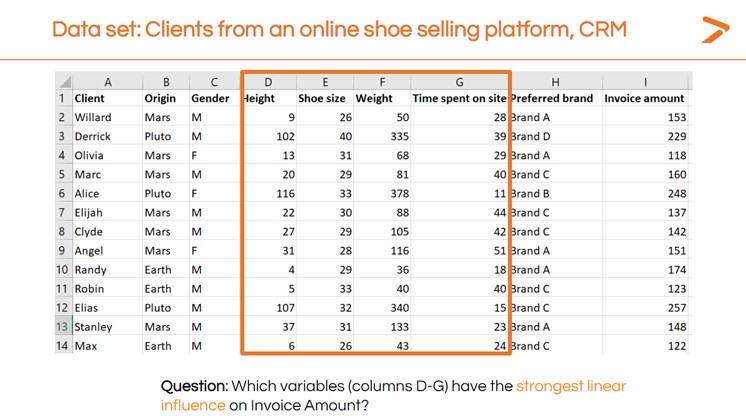
En primer lugar, formule con palabras la pregunta que intenta responder. En el seminario web de XLSTAT, el Dr. Maalouf creó un conjunto de datos de muestra para representar el software de gestión de registros de clientes (CRM) de un minorista de calzado en línea. La pregunta que quería investigar era «¿Cómo varía el importe de la factura en función del tiempo de permanencia?». 

En este ejemplo, la variable que intenta comprender (el importe de la factura) es la variable dependiente. La variable con la que la está comparando (el tiempo en la obra) es la variable independiente. 

INTRODUCCIÓN A LA MODELIZACIÓN DE REGRESIÓN LINEAL: VISUALIZACIÓN INICIAL 

El primer paso para completar una regresión lineal con XLSTAT es obtener una instantánea rápida de cómo se relacionan sus variables dependientes e independientes utilizando una visualización sencilla. El Dr. Maalouf recomienda crear un gráfico de dispersión para este paso inicial. 

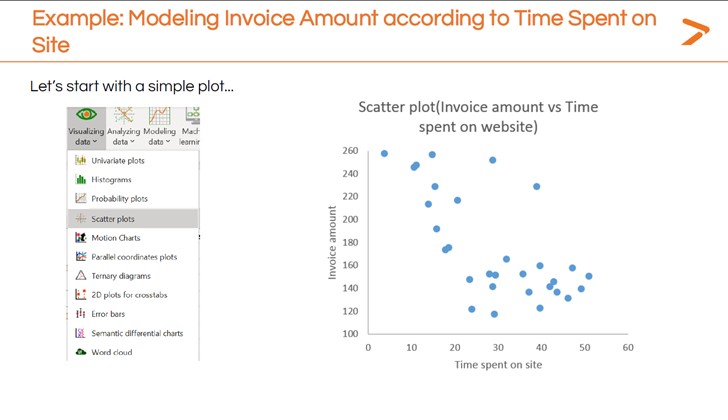
Para generar rápidamente un gráfico de dispersión dentro de XLSTAT: 

• Haga clic en el icono «Visualizar datos» de la barra de herramientas 
• Elija «Gráficos de dispersión» en el menú desplegable 
• En el cuadro de diálogo que aparece, defina las variables que desea que sean dependientes (eje y) e independientes (eje x). 
• Genera el gráfico de dispersión 

El gráfico de dispersión inicial de la imagen anterior parece mostrar que pasar más tiempo en el sitio se correlaciona con un menor valor de la factura. Una modelización más detallada puede dar una descripción más precisa de esta relación. Ahí es donde entra en juego una regresión lineal. 

¿REGRESIÓN LINEAL CON UNA SOLA VARIABLE? 

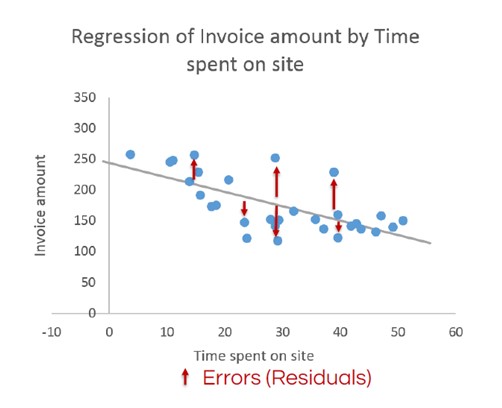
Una regresión lineal es una técnica estadística que traza la relación entre dos variables como una línea recta utilizando un modelo lineal. Al interpretar la regresión, si la línea sube de izquierda a derecha, es un resultado positivo (es decir, a medida que aumenta la variable independiente, también aumenta la variable dependiente). Si la línea desciende de izquierda a derecha, se trata de un resultado negativo (la variable dependiente desciende a medida que aumenta la variable independiente). Una línea más o menos plana significa que hay muy pocos cambios. 

La imagen siguiente muestra la regresión lineal básica calculada para el ejemplo del importe de la factura frente al tiempo de permanencia. No todos los puntos de datos caen sobre la línea resultante. Esos puntos de datos se denominan residuos y se analizarán más adelante en este artículo. Los parámetros de la imagen también pueden denominarse coeficientes de regresión. 

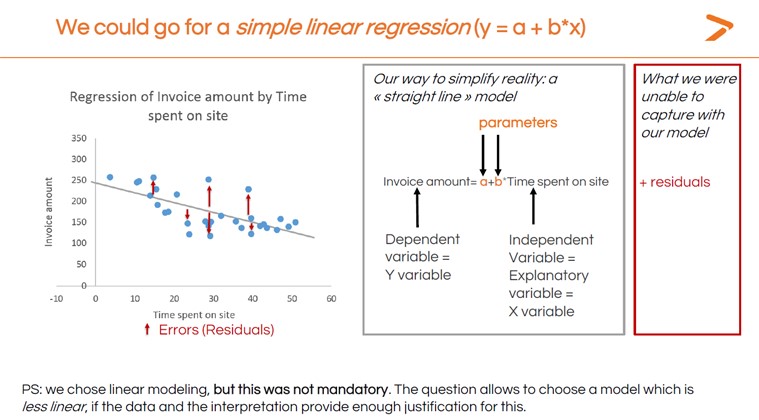
Por ahora, aquí está cómo generar un modelo de regresión lineal simple dentro de XLSTAT.  

1. Haga clic en el icono Modelado de datos de la barra de herramientas 
2. Elija «regresión lineal» en el menú desplegable 
3. En la pestaña «general» del cuadro de diálogo que aparece, elija la columna de su hoja de datos que representa la variable dependiente para el campo «Y/Variables dependientes». 
4. En el campo «X/Variables independientes», seleccione la columna de la hoja de datos que representa la variable independiente. 
5.  Haz clic en «Aceptar». 

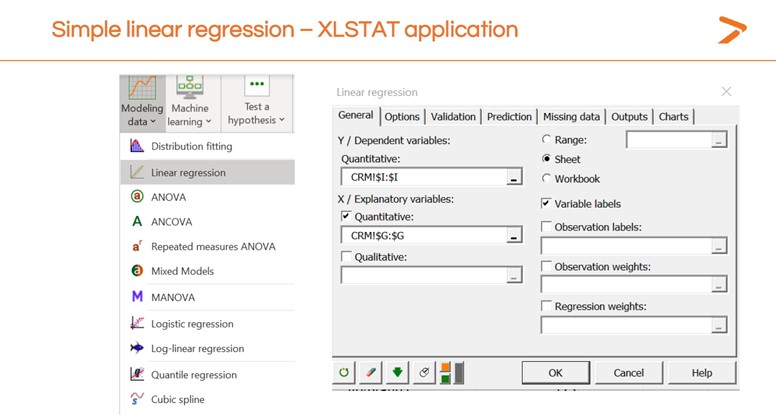
XLSTAT creará una nueva hoja con los resultados de su regresión lineal, tanto en forma de visualización de gráficos como de lectura de datos. Ahora que tiene un resultado, es el momento de interpretarlo y decidir si su modelo es útil. 

INTERPRETACIÓN DEL RESULTADO: TABLA DE PARÁMETROS DEL MODELO 

La primera salida que debe mirar cuando ha creado una regresión lineal en XLSTAT es la tabla de Parámetros del modelo. En ella se muestra el valor p (que es muy bajo, lo que sugiere que el tiempo de permanencia en el sitio sí influye en el importe de las facturas) y otros datos importantes. 

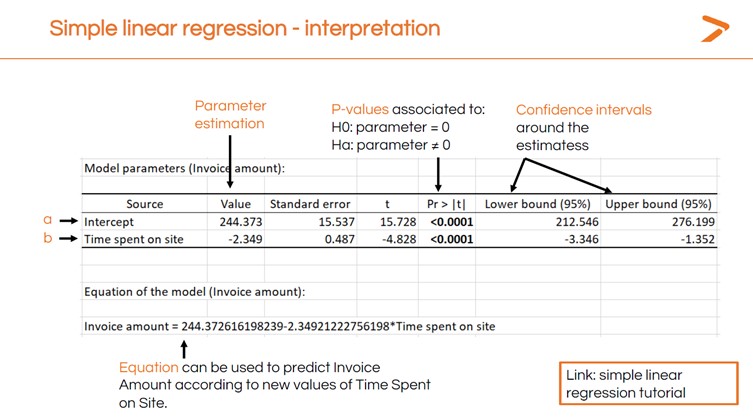
El valor de «intercepción» es el lugar del eje x donde comienza la línea de regresión lineal. Es el valor medio de una factura en el conjunto de datos. El número negativo en el valor de «tiempo de permanencia» muestra que la línea de regresión tendrá una pendiente descendente a un ritmo específico.  

Ahora, si sabe cuánto tiempo pasa un cliente en su sitio, puede predecir el valor de la factura utilizando la siguiente ecuación: 

244,37 - (2,349 x Tiempo en el sitio) = Valor de la factura 

Así, si alguien pasa 25 minutos en el sitio, puede calcular el valor de la factura de esta manera 

244,37 - (2,349 x 25) = 185,65 Valor de la factura 

Ahora tiene un conocimiento específico de la relación entre el tiempo pasado en el sitio y el importe de la factura que puede utilizar para predecir los resultados (y optimizar su sitio web para ayudar a las personas a encontrar más rápidamente lo que quieren comprar). 

La siguiente pregunta es: ¿qué pasa con todos esos residuos? ¿Indican que nuestro modelo es defectuoso de alguna manera? XLSTAT puede ayudarle a validar su modelo investigando los residuos. 

VERIFICACIÓN DEL MODELO: HIPÓTESIS SOBRE LOS RESIDUOS 

Para determinar la validez de una regresión lineal hay que examinar más detenidamente los residuos. Cuando un modelo estadístico es válido, podemos hacer cuatro suposiciones principales sobre los residuos

Podemos comprobar cada uno de ellos planteándonos las siguientes preguntas: 

• ¿Son independientes los residuos, con una medición por individuo? 
• ¿Siguen los residuos una distribución normal en forma de campana? 
• ¿Menos del 5% de los residuos son valores atípicos, es decir, muy alejados de la línea en cualquier dirección? 
• ¿La varianza de los residuos es aproximadamente la misma a lo largo de toda la línea (homocedasticidad)? 

También podemos comprobar cada uno de estos supuestos utilizando XLSTAT. Puede obtener un diagnóstico gráfico rápido de sus residuos en el gráfico Std. Residuales vs. Predicciones que se genera al ejecutar la regresión lineal. 

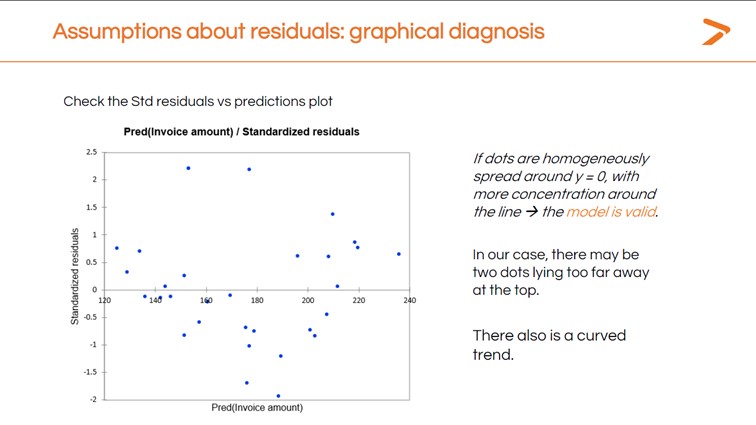
Lo ideal sería que los residuos se agruparan en torno a la línea central de este diagrama. En su lugar, tenemos una tendencia curva con varios puntos que están muy alejados de la línea. 

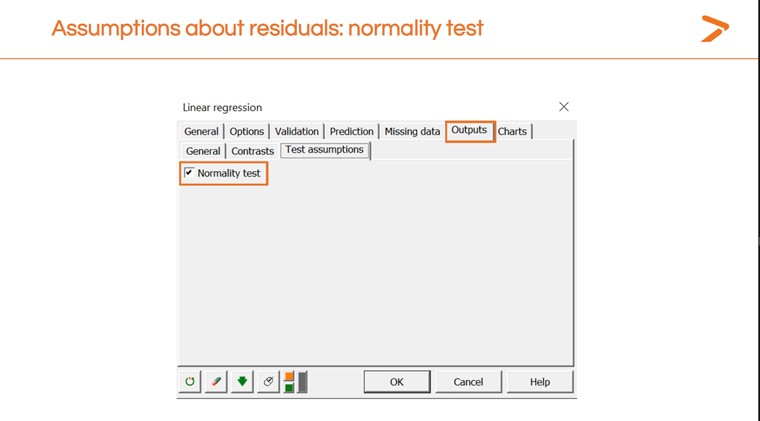
También podemos realizar una comprobación de normalidad en el cuadro de diálogo de regresiones lineales en XLSTAT. 

Esto genera otra tabla de resultados con un valor p. Un valor p más bajo significa que el modelo se ajusta bien; un valor más alto significa que no se ajusta. Los resultados aquí indican que el modelo no se ajusta bien. 

El Dr. Maalouf señaló que las pruebas de normalidad funcionan mejor con grandes conjuntos de datos. Los conjuntos de datos pequeños no dan resultados fiables. Para entender por qué, piense en cada punto de datos como si fuera un píxel en la pantalla de un ordenador. Si sólo tiene unas pocas docenas de píxeles, no podrá saber lo que está viendo. Si tiene miles de ellos, verá una imagen más detallada. 

He aquí otros dos resultados de pruebas de normalidad que ilustran patrones comunes de violación, es decir, patrones de datos en los residuos que indican que puede ser necesario un modelo diferente. 

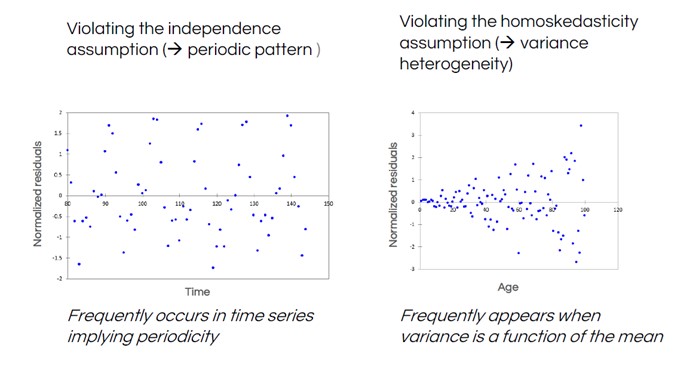
En el gráfico de residuos de la izquierda, vemos una forma de «onda» regular en los datos. Esto es habitual cuando se miden datos en una serie temporal, como los datos meteorológicos: las temperaturas varían previsiblemente en función de la época del año, por lo que no son independientes. El gráfico de la derecha muestra una forma de embudo, lo que indica que la distancia entre los residuos y la línea (la varianza) no es constante.  

XLSTAT puede ayudarle a validar rápidamente su modelo con herramientas para investigar sus residuos. Si observa problemas con sus residuos, tendrá que decidir qué hacer al respecto. 

Fíjese en los valores atípicos. Si hay razones por las que no deberían estar en el conjunto de datos, puede eliminarlos. 

Si sus residuos muestran una clara relación no lineal (como la curva de los datos de nuestra zapatería), considere un tipo de modelo diferente. 

Decida si puede transformar los datos del eje y utilizando transformaciones logarítmicas, de raíz cuadrada o de Box-Cox (todas estas transformaciones están disponibles en XLSTAT). 

EJECUCIÓN Y COMPROBACIÓN DE REGRESIONES LINEALES MÚLTIPLES EN XLSTAT 

Si desea investigar cómo influyen varias variables independientes en su variable dependiente, también puede hacerlo rápidamente en XLSTAT ejecutando una regresión lineal múltiple (MLR). Al configurar su MLR, asegúrese de no elegir demasiadas variables y puntos de datos. Es probable que el modelo que produzca esté «sobreajustado» - es decir, una descripción muy cercana y precisa de su conjunto de datos, pero sólo de su conjunto de datos. No podrá utilizar un modelo sobreajustado para hacer predicciones con los datos.

Seguiremos los mismos pasos que para la regresión lineal simple. En primer lugar, vamos a hacer una visualización rápida.  

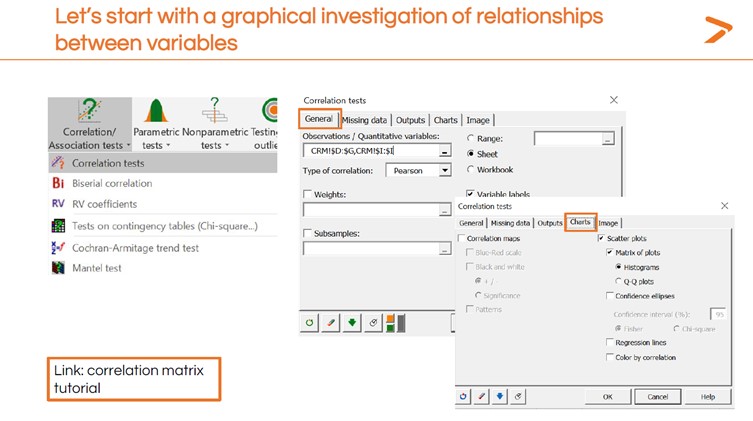
Dado que tenemos múltiples variables, XLSTAT generará múltiples visualizaciones para que podamos examinar las relaciones lineales y correlaciones. En la matriz siguiente, vemos cada variable comparada con las demás. Hay algunos patrones sorprendentes. 

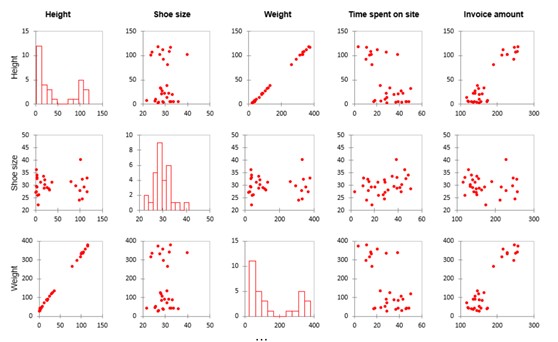
Fíjese en los fuertes gráficos de dispersión en forma de línea en las filas de peso y altura. Esto indica que estas variables muestran básicamente los mismos datos (por ejemplo, el tamaño de una persona). Llamamos variables multicolineales a los puntos de datos que miden el mismo factor. Puede eliminar una u otra de su modelo. Si no lo hace, los coeficientes de su modelo no serán estables y las pruebas no serán buenas. Esto se denomina problema de multicolinealidad.  

También puede generar una comprobación de multicolinealidad al ejecutar la regresión lineal múltiple en XLSTAT haciendo clic en la pestaña «Resultados» y marcando la casilla «Estadísticas de multicolinealidad». 

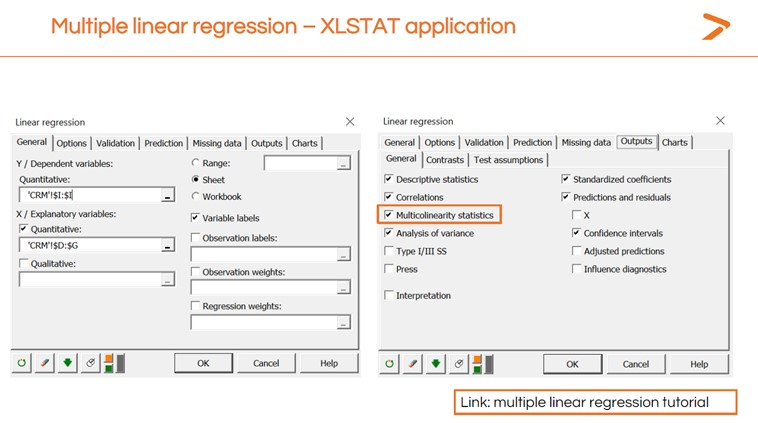
Las estadísticas de multicolinealidad incluyen un factor de inflación de la varianza (VIF) para determinar lo redundante que es cualquier variable explicativa en comparación con otras. Un número elevado indica que debe eliminar la variable redundante y relanzar su MLR. 

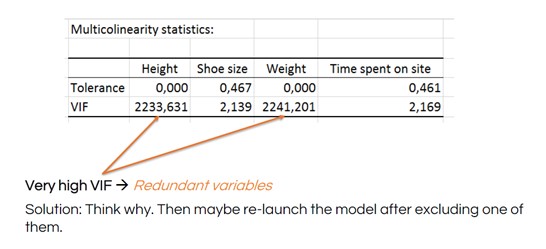
Observe cómo descienden las cifras de VIF tras eliminar la altura de la MLR: 

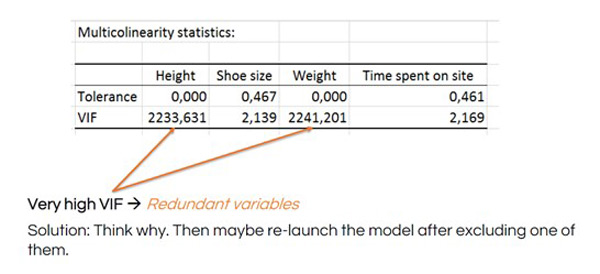
Después de ejecutar su MLR, querrá comprobar los residuos de la misma forma que lo hizo para la regresión lineal simple. En este caso, tener más variables nos muestra diferentes patrones en los residuos que podrían apuntar a otras técnicas de modelado estadístico que podríamos probar. . 

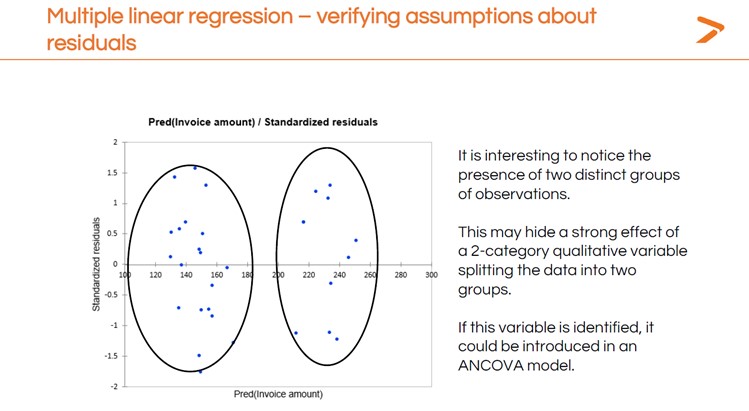
También querrá interpretar los resultados de la MLR para responder a su pregunta: ¿qué variable tiene un mayor impacto en el importe de la factura? 

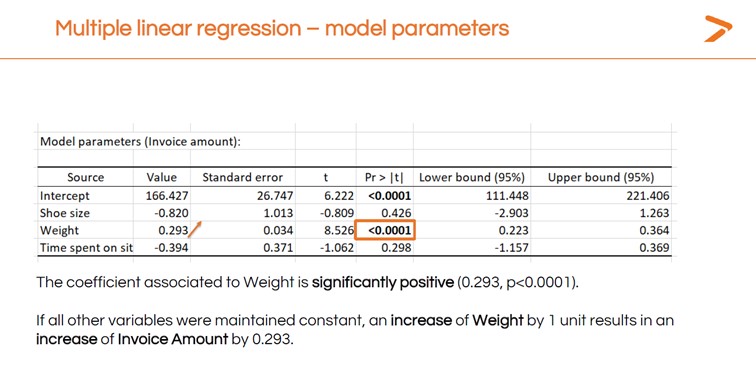
Estos resultados del análisis de regresión lineal sugieren que el peso es la única variable con un impacto positivo fuerte y significativo en el importe de la factura, ya que es la única variable con una prueba significativa. 

MÁS INFORMACIÓN SOBRE REGRESIÓN LINEAL MÚLTIPLE Y SIMPLE CON XLSTAT 

¿Está interesado en obtener más información sobre las potentes herramientas de modelado estadístico, como el análisis de regresión, que XLSTAT aporta a su espacio de trabajo de Microsoft Excel? Solicite una demostración gratuita hoy mismo. También puede visitar el canal de YouTube de XLSTAT para ver más vídeos tutoriales.