Analyse de régression : Adapter la méthode aux données

Qu'est-ce que l'analyse de régression ?

L'analyse de régression est l'une des pierres angulaires des méthodes statistiques utilisées dans l'analyse des données et la modélisation prédictive. Il s'agit d'une technique statistique puissante conçue pour examiner la relation entre les variables, ce qui en fait un outil essentiel dans des domaines tels que l'économie, la biologie, les sciences sociales, etc.

L'objectif principal de l'analyse de régression est de déterminer comment les changements dans les variables indépendantes influencent la variable dépendante - ce qui permet de mieux comprendre les mécanismes sous-jacents des données afin de faire de meilleures prédictions et de prendre de meilleures décisions.

Quels sont les différents types d'analyse de régression ?

La polyvalence des modèles de régression permet de les appliquer à un large éventail de types de données et de scénarios de recherche. Cependant, différents types de modèles de régression sont spécifiquement adaptés pour traiter des types distincts de données et de relations, ce qui rend essentiel le choix du bon modèle en fonction de la nature des données et des objectifs de la recherche.

Que les données soient continues, catégorielles, binaires ou basées sur le nombre, chaque type de méthode de régression est conçu pour répondre aux objectifs de la recherche et aux qualités uniques de l'ensemble de données. Par exemple, alors que la régression linéaire est idéale pour modéliser des relations directes entre des variables continues, la régression logistique est mieux adaptée aux résultats binaires ou catégoriels. De même, lorsque l'on travaille avec des données complexes et de haute dimension, des techniques plus avancées telles que la régression des moindres carrés partiels (PLS), la régression Ridge et la régression Lasso peuvent s'avérer nécessaires.

Quel est le bon modèle de régression pour votre analyse de données ?

Le choix d'un mauvais modèle de régression peut conduire à des conclusions inexactes et à des performances prédictives médiocres. Pour déterminer le bon modèle pour vos données, vous devez comprendre les forces, les faiblesses et les applications appropriées de chaque type de modèle de régression.

Dans ce guide de l'analyse de régression, nous allons discuter des différents types de régression, mettre en évidence les types de données pour lesquels ils sont les mieux adaptés, et illustrer leurs applications pratiques dans divers secteurs d'activité.

Téléchargez votre version d'évaluation gratuite de XLSTAT pour commencer à appliquer ces modèles de régression à vos données.

1. Régression linéaire

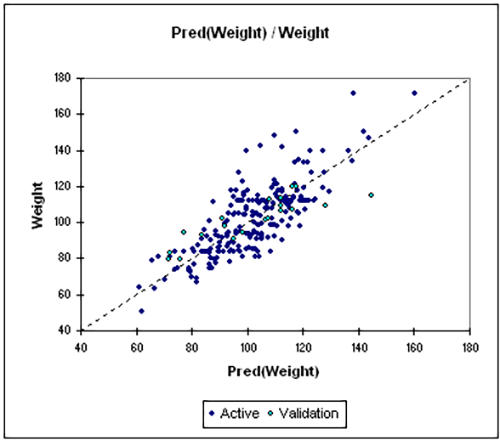
• Type de données : Variable dépendante continue avec une ou plusieurs variables indépendantes continues.
• Description : La régression linéaire (y compris la régression linéaire simple et la régression linéaire multiple) examine la relation entre une variable dépendante et une ou plusieurs variables indépendantes. Elle suppose une relation linéaire et est utilisée lorsque le résultat et les prédicteurs sont continus. L'objectif est de prédire ou d'expliquer la variable dépendante à l'aide des variables prédictives. Ce modèle permet d'analyser l'effet combiné de plusieurs facteurs sur le résultat.
• Exemple : Estimation de l'influence du revenu et de l'âge sur les habitudes de consommation.

En savoir plus sur l'analyse de régression linéaire

2. Régression logistique

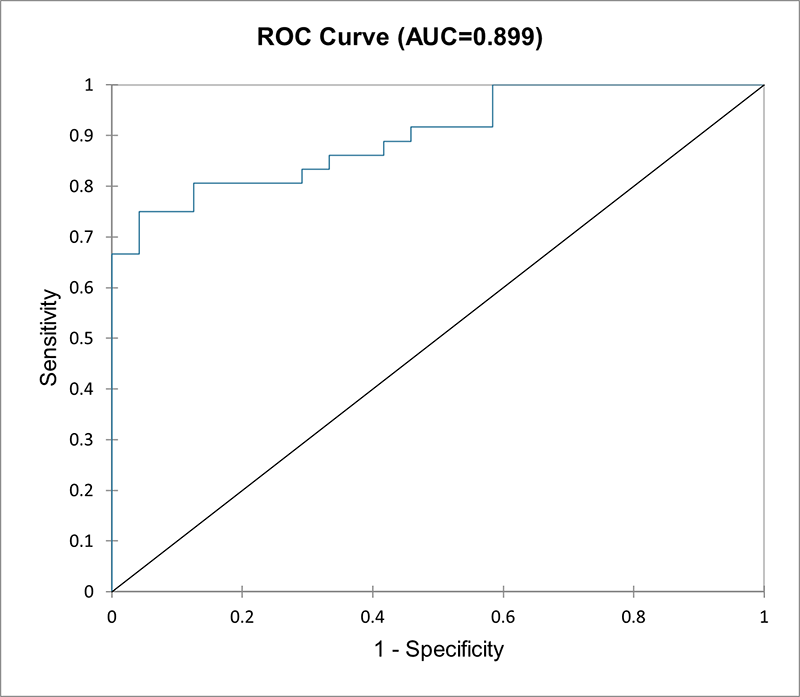
• Type de données : Variable dépendante binaire ou catégorielle (0 ou 1). La régression logistique multinomiale est également possible si la variable dépendante a plus de 2 catégories. Variables indépendantes continues ou catégorielles.
• Description : La régression logistique est utilisée lorsque la variable dépendante est catégorique (par exemple, succès/échec, oui/non, petit/moyen/grand). La sortie est modélisée à l'aide d'une fonction logistique qui prédit les probabilités des différents résultats.
• Exemple : Prévoir si un client achètera un produit (oui/non) en fonction de son revenu, de son âge et de son comportement d'achat antérieur.

En savoir plus sur la régression logistique

3. Régression par moindres carrés partiels (PLS)

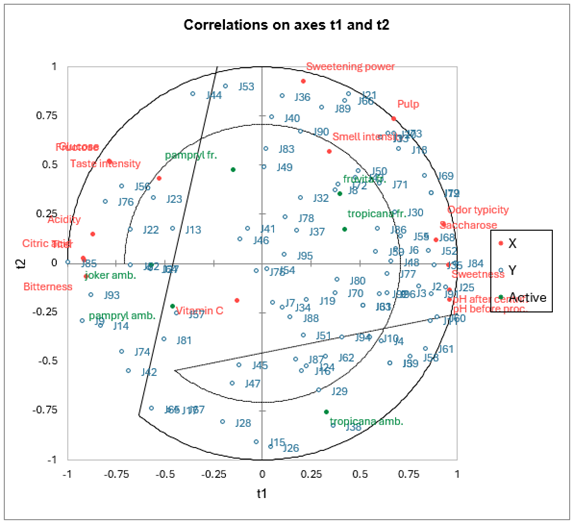
• Type de données : Données multivariées avec des prédicteurs à haute dimension (colinéaires et bruyants). Variables indépendantes continues ou catégorielles.
• Description : La régression PLS est particulièrement utile lorsque les variables prédictives sont fortement colinéaires (c'est-à-dire qu'elles sont fortement corrélées entre elles) ou lorsque le nombre de prédicteurs est supérieur au nombre d'observations. La PLS combine les caractéristiques de l'analyse en composantes principales (ACP) et de la régression multiple en projetant les variables prédictives dans un nouvel espace et en trouvant une relation linéaire entre ces projections et la variable dépendante.
• Application : La PLS est largement utilisée en chimiométrie, en bioinformatique et dans d'autres domaines traitant d'ensembles de données à haute dimension.
• Exemple : Prédiction des propriétés chimiques d'un composé sur la base d'un vaste ensemble de mesures spectroscopiques.

En savoir plus sur la régression par moindres carrés partiels >>.

4. Régression Ridge, Lasso et Elastic Net

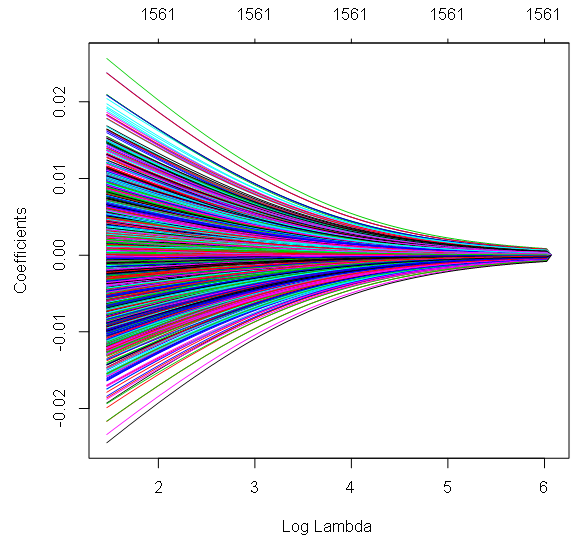
• Type de données : Variable dépendante continue avec de nombreuses variables prédictives (éventuellement corrélées). Variables indépendantes continues ou catégorielles.
• Description : Il s'agit de techniques de régularisation qui modifient la fonction de perte afin d'éviter l'ajustement excessif, en particulier en cas de multicolinéarité. La régression Ridge pénalise la somme des carrés des coefficients, tandis que la régression Lasso pénalise la valeur absolue des coefficients, ce qui conduit souvent certains coefficients à zéro. L'Elastic Net est un mélange de ces deux méthodes.
• Exemple : La régression ridge est souvent utilisée en génomique pour prédire le risque de maladie sur la base de milliers de marqueurs génétiques.

En savoir plus sur la régression Ridge >>

En savoir plus sur la régression Lasso >>

5. Régression log-linéaire (ou de Poisson)

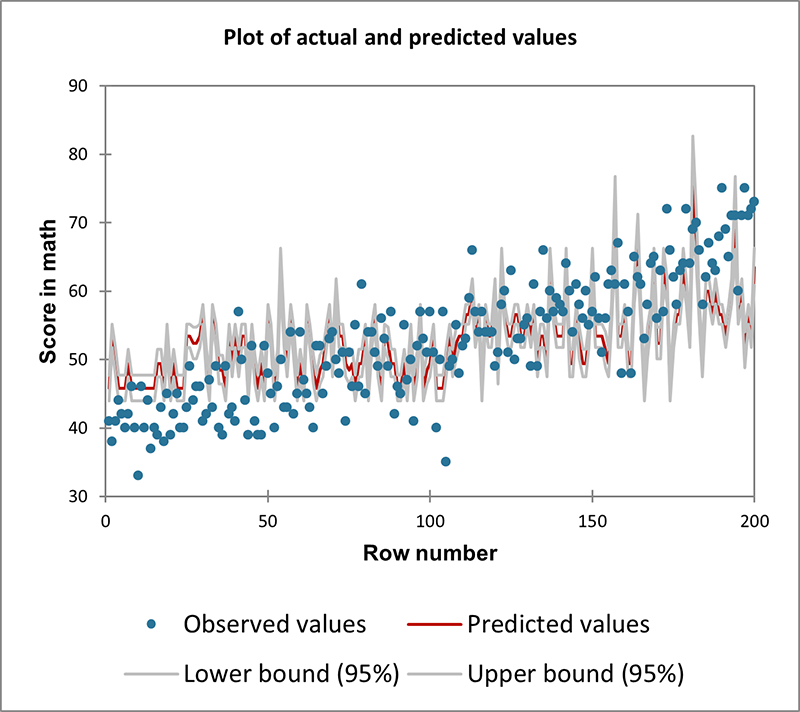
• Type de données : Données de comptage (nombre d'occurrences d'un événement). Variables indépendantes continues ou catégorielles.
• Description : La régression de Poisson est idéale pour modéliser les données de comptage et les taux, en particulier lorsque le résultat représente le nombre d'occurrences d'un événement dans un intervalle fixe (par exemple, le temps, la distance).
• Exemple : Modélisation du nombre d'appels reçus par un centre d'appels en fonction de l'heure de la journée et du nombre d'opérateurs en service.

Pour en savoir plus sur la régression log-linéaire >>.

6. Régression quantile

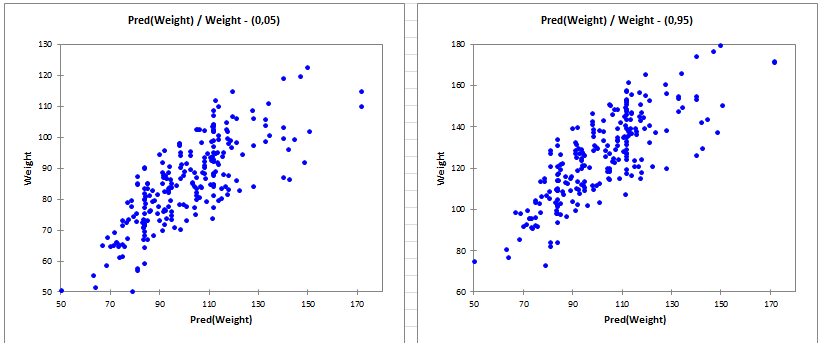
• Type de données : Variable dépendante continue avec des relations hétérogènes entre les quantiles.
• Description : Contrairement à la régression linéaire qui estime la moyenne de la variable dépendante conditionnellement aux variables prédictives, la régression quantile estime la médiane conditionnelle ou d'autres quantiles de la variable dépendante. Elle est donc utile lorsque la relation entre les variables varie entre les différents points de la distribution, au lieu d'être constante sur l'ensemble des données.
• Application : La régression quantile est particulièrement efficace lorsque les données présentent une variance non constante ou lorsque des valeurs aberrantes influencent des parties spécifiques de la distribution.
• Exemple : Étude de l'impact de l'éducation sur les différents quantiles de la distribution des revenus, lorsque des facteurs peuvent influencer différemment les segments inférieur, moyen et supérieur.

En savoir plus sur la régression des quantiles

7. Régression non paramétrique (Kernel et Lowess)

• Type de données : Données complexes sans relation fonctionnelle prédéfinie entre les variables.
• Description : La régression non paramétrique ne suppose pas de forme fonctionnelle spécifique pour la relation entre les variables indépendantes et dépendantes. Au lieu de cela, elle permet aux données de déterminer la forme de la relation. Les régressions polynomiales sont couramment utilisées dans les méthodes non paramétriques.
• Application : Ces méthodes sont utiles lorsque l'on dispose de peu de connaissances préalables sur la forme fonctionnelle de la relation entre les variables ou lorsque les données sont très flexibles ou complexes.
• Exemple : Modélisation de la relation entre la température et la croissance des plantes lorsque la relation peut varier de manière non linéaire entre différentes plages de température.

Pour en savoir plus sur la régression non paramétrique >>.

8. Régression non linéaire

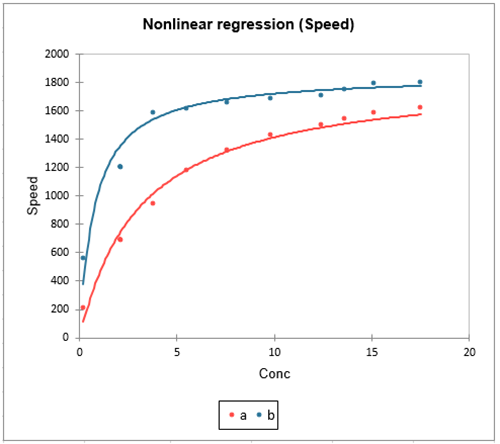
• Type de données : Variable dépendante continue avec une relation non linéaire entre les variables.
• Description : La régression non linéaire est utilisée lorsque la relation entre les variables dépendantes et indépendantes ne peut pas être correctement saisie par une équation linéaire. Le modèle peut prendre différentes formes telles que des relations exponentielles, logarithmiques ou polynomiales. La régression non linéaire nécessite des méthodes itératives pour l'estimation des paramètres car ceux-ci ne peuvent souvent pas être résolus explicitement.
• Application : Elle est souvent appliquée dans des domaines tels que la biologie, l'économie et l'ingénierie, où les relations sont intrinsèquement non linéaires.
• Exemple : Modélisation de la croissance d'une population au fil du temps à l'aide d'une courbe de croissance logistique, où la croissance s'accélère au début mais ralentit lorsque la population atteint la capacité de charge de l'environnement.

En savoir plus sur la régression non linéaire

Commencez à mettre l'analyse de régression à votre service

Le choix de la meilleure analyse de régression ne doit pas être décourageant. Avec les bons outils, vous pouvez facilement explorer et appliquer ces méthodes à vos données sans avoir besoin d'une formation statistique approfondie. Pour vous aider à démarrer, nous vous offrons une version d'évaluation gratuite de 14 jours de XLSTAT - un logiciel statistique puissant et convivial qui peut vous aider à obtenir des informations plus approfondies et à améliorer la fiabilité de vos recherches et de vos décisions commerciales.

Télécharger la version d'évaluation gratuite de XLSTAT