Comment créer et valider des régressions linéaires simples et multiples dans XLSTAT ?

Si vous êtes comme la plupart des chercheurs et des analystes de données, vous vous retrouvez probablement dans des situations où vous devez prédire les tendances futures, identifier les principaux influenceurs d'un résultat ou simplement comprendre le lien entre les variables. Dans ces cas, la régression linéaire est un outil fondamental pour tous ceux qui essaient de comprendre les relations entre leurs données et de faire des prédictions sur la base de ces informations. Cependant, l'utilisation de la régression linéaire peut s'avérer décourageante, en particulier pour les novices en matière d'analyse statistique. 

C'est là que des outils d'analyse statistique conviviaux comme XLSTAT et une formation complète deviennent essentiels, comblant le fossé entre le besoin de méthodes statistiques avancées et la facilité de les mettre en œuvre efficacement. 

Dans l'un de nos webinaires, Jean-Paul Maalouf, consultant en science des données, a expliqué aux participants le pourquoi et le comment de l'utilisation d'un modèle de régression linéaire - tout en démontrant comment XLSTAT peut aider à vérifier les erreurs courantes dans ce type de modélisation.  

Regardez le webinaire ou continuez à lire pour apprendre comment créer et valider des régressions linéaires simples et multiples dans XLSTAT avec Jean-Paul Maalouf. 

À PROPOS DU LOGICIEL STATISTIQUE XLSTAT 

Comme nous allons discuter de l'utilisation de XLSTAT pour la modélisation de la régression linéaire, il peut être utile de se familiariser avec les fonctionnalités générales de ce puissant logiciel statistique. XLSTAT peut vous aider à optimiser et à rationaliser vos analyses statistiques, tout en fonctionnant au sein de Microsoft Excel. XLSTAT met à votre disposition plus de 300 fonctions pour l'analyse, la modélisation et la visualisation des données, et ces fonctions se répartissent en différentes catégories d'outils : 

• Descriptive - Expliquer des variables uniques ou des liens entre deux variables (par exemple, trouver la moyenne ou l'écart-type d'un ensemble de données). 
• Exploratoire - recherche de modèles dans de grands ensembles de données  
• Tests statistiques - Analyse des données afin de prouver ou d'infirmer une hypothèse. 
• Modélisation statistique - Comprendre comment une variable se comporte sous l'influence d'autres variables, puis utiliser cette relation, souvent exprimée par une équation de régression, pour faire des prédictions. 
• Préparation des données - Processus consistant à préparer les données brutes en vue de leur analyse. 
• Visualisation des données - Utilisation de graphiques et de tableaux pour représenter les informations sur les données. 
• L'apprentissage automatique - L'utilisation de l'intelligence artificielle pour apprendre à partir des données et prédire les résultats. 

De plus, XLSTAT contient des fonctionnalités avancées spécifiques aux domaines de l'analyse sensorielle, des études de marché, des sciences de la vie et de la qualité.  

Dans cet article, nous nous concentrerons sur les tests statistiques et la modélisation statistique. Pour en savoir plus sur les autres fonctions de XLSTAT, consultez nos tutoriels. 

QU'EST-CE QUE LA MODÉLISATION STATISTIQUE ET LES TESTS STATISTIQUES ? 

Pour commencer, un modèle statistique est une représentation simplifiée de la réalité à l'aide de données, impliquant souvent une analyse de régression pour établir des relations linéaires. La modélisation statistique permet de comprendre comment une variable se comporte lorsque d'autres variables changent. Une fois que nous disposons d'un modèle statistique dont l'exactitude et l'utilité ont été vérifiées, nous pouvons l'utiliser pour faire des prédictions sur les résultats en utilisant de nouvelles données. 

Les tests statistiques consistent à utiliser des modèles statistiques pour prouver ou réfuter une hypothèse. D'une manière générale, les tests statistiques tentent de déterminer si la variable A change de manière significative lorsqu'elle est affectée par la variable B. Cela conduit à deux résultats possibles : 

• L'hypothèse nulle : Il n'y a pas de changement significatif de la variable A par rapport à la variable B. 
• L'hypothèse alternative : Il y a un changement significatif de la variable A par rapport à la variable B. 

Les tests statistiques aboutissent à un nombre appelé valeur de probabilité, ou valeur p. La valeur p exprime le degré de probabilité d'un changement de la variable A par rapport à la variable B. La valeur p exprime la probabilité que l'hypothèse nulle soit vraie, c'est-à-dire la probabilité qu'il n'y ait pas de changement significatif. La valeur p est un nombre compris entre 0 et 1. Plus la valeur est proche de 1, moins le résultat est significatif. Chaque test statistique exige des chercheurs qu'ils fixent leur propre seuil de valeur p. 

COMMENT CHOISIR UNE MÉTHODE DE MODÉLISATION STATISTIQUE POUR MES DONNÉES ? 

Il existe de très nombreux types de modèles statistiques. La méthode que vous choisirez dépendra des données dont vous disposez et de ce que vous voulez en comprendre. Le Dr Maalouf a expliqué quelques-unes des méthodes de modélisation les plus courantes pour différents types de variables. 

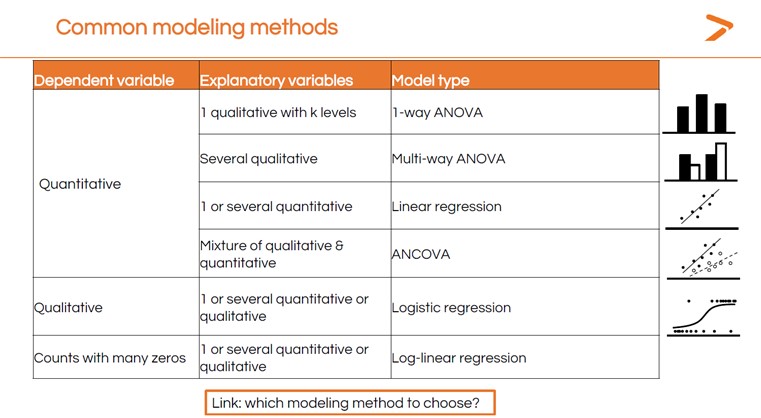
Avec autant d'options, il peut être difficile de choisir le bon test statistique pour votre analyse. C'est là que l'outil MyAssistant de XLSTAT peut vous aider. Il vous suffit de répondre à une série de questions, et MyAssistant vous orientera vers le bon test pour votre analyse de données. Nous vous proposons également un petit guide de la modélisation statistique qui peut vous aider à choisir la méthode de modélisation à utiliser dans XLSTAT en fonction de vos données et de l'objectif de votre analyse.  

COMMENT DÉTERMINER QUELLES SONT LES VARIABLES DÉPENDANTES OU INDÉPENDANTES ? 

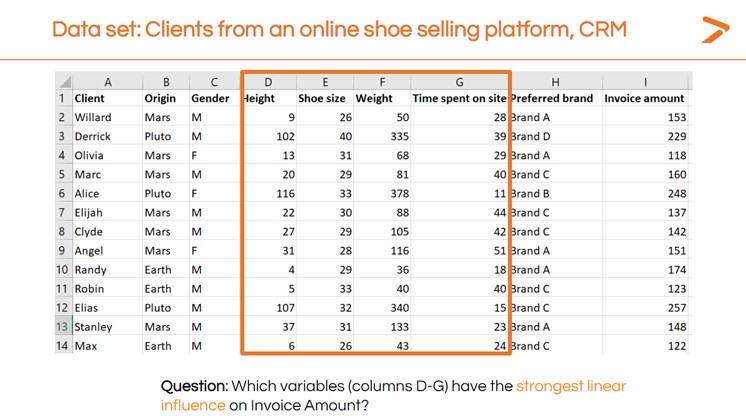
Tout d'abord, il faut formuler la question à laquelle vous essayez de répondre avec des mots. Dans le webinaire XLSTAT, le Dr. Maalouf a créé un ensemble de données représentatif du logiciel de gestion des dossiers clients (CRM) d'un détaillant de chaussures en ligne. La question qu'il souhaitait étudier était la suivante : « Comment le montant de la facture varie-t-il en fonction de la taille de l'entreprise ? « Comment le montant de la facture varie-t-il en fonction du temps passé sur le site ? ». 

Dans cet exemple, la variable que vous essayez de comprendre (le montant de la facture) est la variable dépendante. La variable à laquelle vous la comparez (le temps passé sur le site) est la variable indépendante. 

DÉBUT DE LA MODÉLISATION DE LA RÉGRESSION LINÉAIRE : VISUALISATION INITIALE 

La première étape d'une régression linéaire avec XLSTAT est d'obtenir un aperçu rapide de la relation entre les variables dépendantes et indépendantes à l'aide d'une visualisation simple. Maalouf recommande de créer un diagramme de dispersion pour cette première étape. 

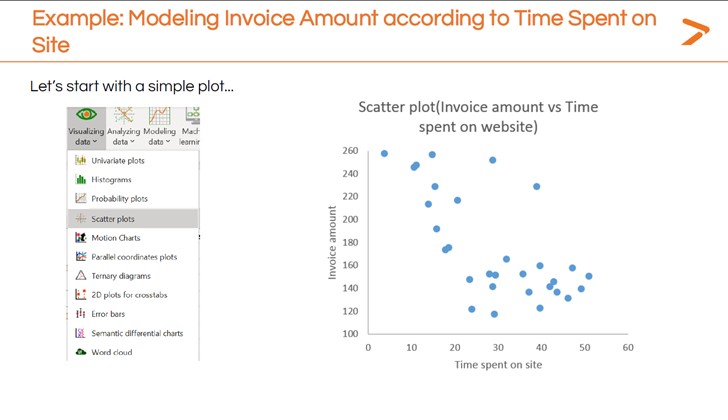
Pour générer rapidement un nuage de points dans XLSTAT : 

• Cliquez sur l'icône « Visualisation des données » dans la barre d'outils 
• Choisissez « Diagramme de dispersion » dans le menu déroulant 
• Dans la boîte de dialogue qui apparaît, définissez les variables dépendantes (axe des ordonnées) et indépendantes (axe des abscisses). 
• Générer le diagramme de dispersion 

Le diagramme de dispersion initial de l'image ci-dessus semble montrer que le fait de passer plus de temps sur le site est corrélé à une valeur de facture plus faible. Une modélisation plus poussée peut donner une description plus précise de cette relation. C'est là qu'intervient la régression linéaire. 

RÉGRESSION LINÉAIRE À UNE SEULE VARIABLE ? 

La régression linéaire est une technique statistique qui permet de tracer la relation entre deux variables sous la forme d'une ligne droite à l'aide d'un modèle linéaire. Lors de l'interprétation d'une régression, si la ligne monte de gauche à droite, il s'agit d'un résultat positif (c'est-à-dire que la variable indépendante augmente, tout comme la variable dépendante). Si la ligne descend de gauche à droite, il s'agit d'un résultat négatif (la variable dépendante diminue lorsque la variable indépendante augmente). Une ligne plus ou moins plate signifie qu'il y a très peu de changement. 

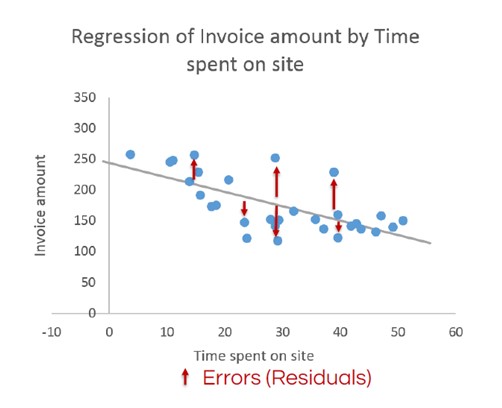
L'image ci-dessous montre la régression linéaire de base calculée pour l'exemple du montant de la facture en fonction du temps passé sur le site. Tous les points de données ne se situent pas sur la ligne obtenue. Ces points de données sont appelés résidus et seront examinés plus loin dans cet article. Les paramètres de l'image peuvent également être appelés coefficients de régression. 

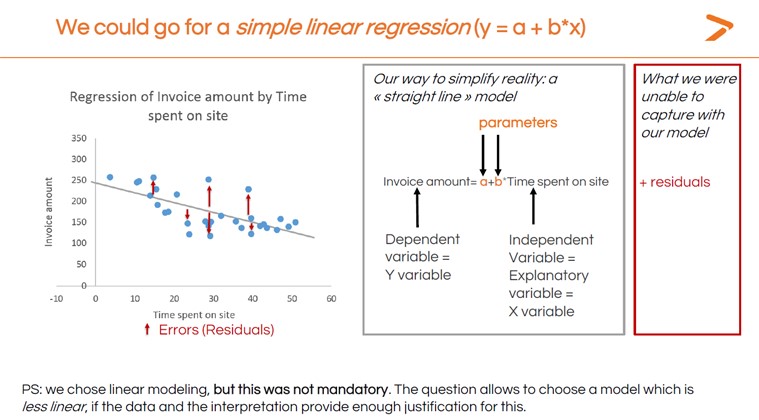
Pour l'instant, voici comment générer un modèle de régression linéaire simple dans XLSTAT.  

1. Cliquez sur l'icône « Modélisation des données » dans la barre d'outils. 
2. Choisissez « Régression linéaire » dans le menu déroulant. 
3. Dans l'onglet « général » de la boîte de dialogue qui apparaît, choisissez la colonne de votre feuille de données qui représente la variable dépendante pour le champ « Y/Variables dépendantes ». 
4. Choisissez la colonne de votre feuille de données qui représente la variable indépendante pour le champ « X/Variables indépendantes ». 
5.  Cliquez sur « OK » 

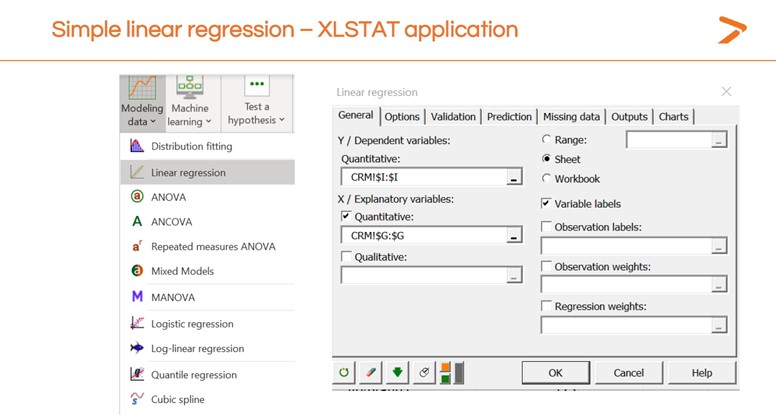
XLSTAT va créer une nouvelle feuille avec les résultats de votre régression linéaire, à la fois sous forme de graphique et sous forme de données. Maintenant que vous avez un résultat, il est temps de l'interpréter et de décider si votre modèle est utile. 

INTERPRÉTATION DES RÉSULTATS : TABLEAU DES PARAMÈTRES DU MODÈLE 

La première sortie à regarder lorsque vous avez créé une régression linéaire dans XLSTAT est le tableau des paramètres du modèle. Ce tableau indique la valeur p (qui est très faible, ce qui suggère que le temps passé sur le site a un impact sur le montant des factures) et d'autres données importantes. 

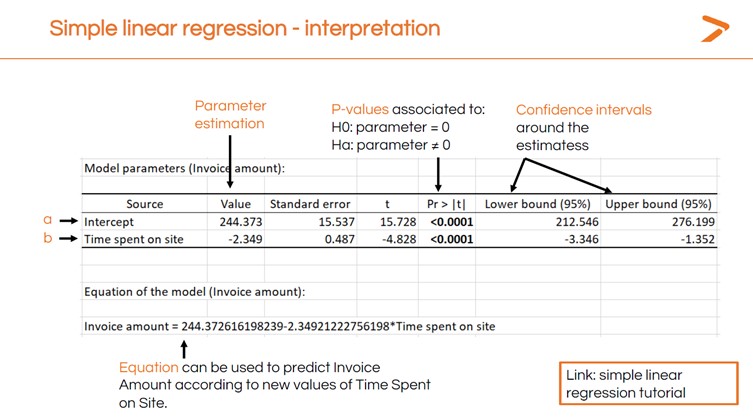
La valeur « intercept » est l'endroit de l'axe des x où commence la ligne de régression linéaire. Il s'agit de la valeur moyenne d'une facture dans l'ensemble des données. Le nombre négatif de la valeur « temps passé sur le site » indique que la ligne de régression s'incline vers le bas à un taux spécifique.  

Maintenant, si vous savez combien de temps un client passe sur votre site, vous pouvez prédire la valeur de la facture à l'aide de l'équation suivante : 

244,37 - (2,349 x Temps passé sur le site) = Valeur de la facture 

Ainsi, si un client passe 25 minutes sur le site, vous pouvez calculer la valeur de la facture de la manière suivante : 

244,37 - (2,349 x 25) = 185,65 Valeur de la facture 

Vous avez maintenant une idée précise de la relation entre le temps passé sur le site et le montant de la facture, que vous pouvez utiliser pour prédire les résultats (et optimiser votre site web pour aider les gens à trouver plus rapidement ce qu'ils veulent acheter). 

La question suivante est la suivante : qu'en est-il de tous ces résidus ? Indiquent-ils que notre modèle est défectueux ? XLSTAT peut vous aider à valider votre modèle en étudiant les résidus. 

VÉRIFICATION DU MODÈLE : HYPOTHÈSES SUR LES RÉSIDUS 

Pour déterminer la validité d'une régression linéaire, il faut examiner de plus près les résidus. Il y a quatre hypothèses principales que l'on peut faire sur les résidus lorsqu'un modèle statistique est valide

Nous pouvons vérifier chacun de ces points en posant les questions suivantes : 

• Les résidus sont-ils indépendants, avec une mesure par individu ? 
• Les résidus suivent-ils une distribution normale en forme de cloche ? 
• Moins de 5 % des résidus sont-ils aberrants, c'est-à-dire très éloignés de la ligne dans un sens ou dans l'autre ? 
• La variance des résidus reste-t-elle à peu près la même tout au long de la ligne (homoscédasticité) ? 

Nous pouvons également vérifier chacune de ces hypothèses à l'aide de XLSTAT. Vous pouvez obtenir un diagnostic graphique rapide de vos résidus à partir du graphique Std. Résidus vs. Prédictions qui est généré lorsque vous effectuez votre régression linéaire. 

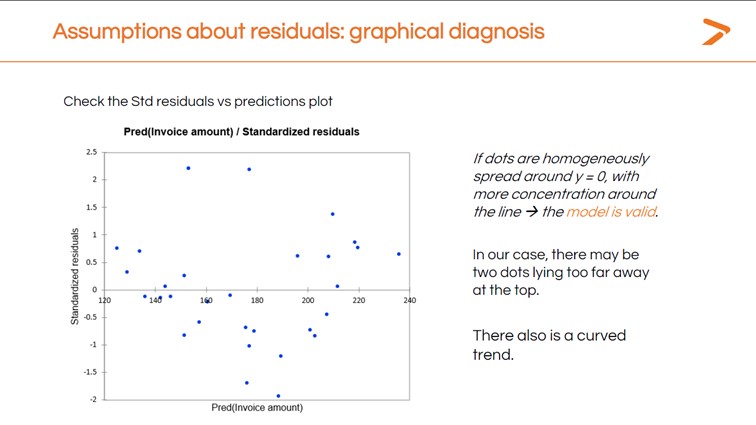
Idéalement, les résidus devraient être regroupés autour de la ligne centrale de ce graphique. Au lieu de cela, nous avons une tendance courbe avec plusieurs points très éloignés de la ligne. 

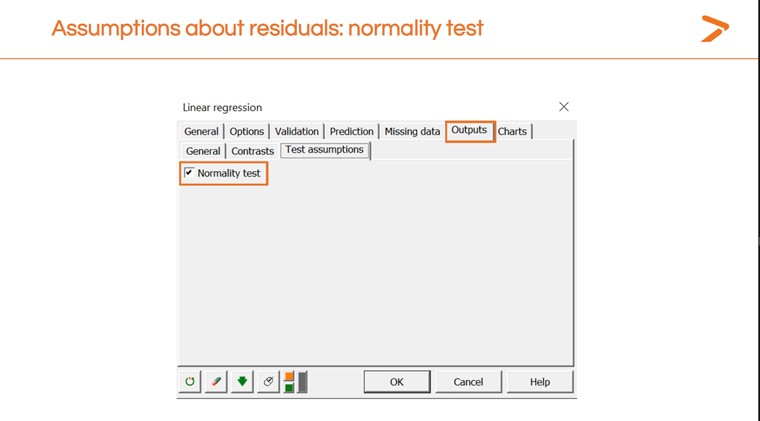
Nous pouvons également effectuer un contrôle de normalité à partir de la boîte de dialogue « Régressions linéaires » de XLSTAT. 

Cela génère un autre tableau de résultats avec une p-valeur. Une valeur p plus faible signifie que le modèle est bien ajusté ; une valeur p plus élevée signifie qu'il ne l'est pas. Les résultats ici indiquent que le modèle n'est pas bien ajusté. 

Le Dr. Maalouf a souligné que les tests de normalité fonctionnent mieux avec des ensembles de données plus importants. Les petits ensembles de données ne donneront pas de résultats fiables. Pour comprendre pourquoi, imaginez que chaque point de données est un pixel sur un écran d'ordinateur. Si vous n'avez que quelques dizaines de pixels, vous ne pourrez pas savoir ce que vous regardez. Si vous en avez des milliers, vous verrez une image plus détaillée. 

Voici deux autres résultats de tests de normalité qui illustrent des schémas courants de violation - c'est-à-dire des schémas de données dans les résidus qui indiquent qu'un modèle différent peut être nécessaire. 

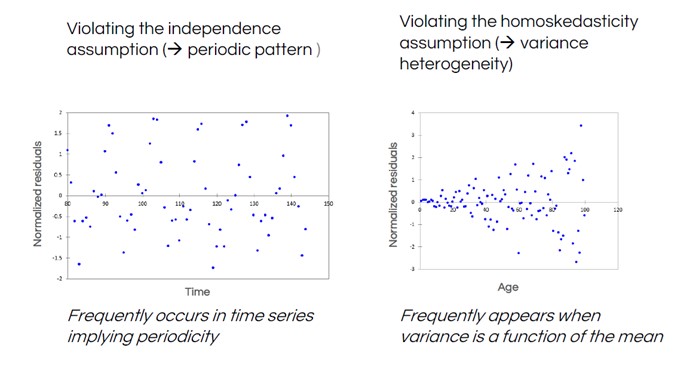
Dans le graphique des résidus de gauche, on observe une forme de « vague » régulière dans les données. Ce phénomène est courant lorsque l'on mesure des données dans une série chronologique, comme les données météorologiques - les températures varient de manière prévisible en fonction de la période de l'année, et ne sont donc pas indépendantes. Le graphique de droite montre une forme d'entonnoir, indiquant que la distance entre les résidus et la droite (la variance) n'est pas constante.  

XLSTAT peut vous aider à valider rapidement votre modèle grâce à des outils permettant d'étudier vos résidus. Si vous constatez des problèmes avec vos résidus, vous devrez décider de ce qu'il faut faire. 

Examinez les valeurs aberrantes. S'il existe des raisons pour lesquelles elles ne devraient pas figurer dans l'ensemble des données, vous pouvez les éliminer. 

Si vos résidus présentent une relation non linéaire évidente (comme la courbe de nos données sur les magasins de chaussures), envisagez un autre type de modèle. 

Décidez si vous pouvez transformer vos données en ordonnées en utilisant les transformations logarithme, racine carrée ou Box-Cox (toutes ces transformations sont disponibles dans XLSTAT). 

EXÉCUTER ET VÉRIFIER DES RÉGRESSIONS LINÉAIRES MULTIPLES DANS XLSTAT 

Si vous souhaitez étudier l'influence de plusieurs variables indépendantes sur votre variable dépendante, vous pouvez également le faire rapidement dans XLSTAT en effectuant une régression linéaire multiple (MLR). Lorsque vous mettez en place votre MLR, assurez-vous de ne pas choisir trop de variables et de points de données. Le modèle que vous obtiendrez sera probablement « sur-ajusté » - c'est-à-dire une description très proche et précise de votre ensemble de données, mais seulement de votre ensemble de données. Vous ne pourrez pas utiliser un modèle surajusté pour faire des prédictions.

Nous suivrons les mêmes étapes que pour la régression linéaire simple. Commençons par une visualisation rapide.  

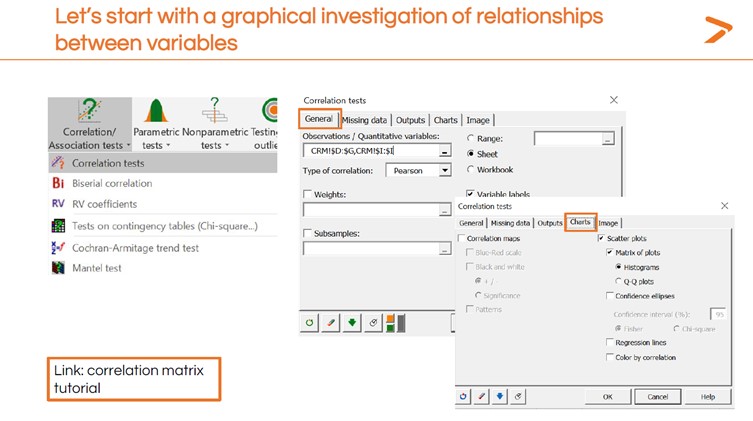
Comme nous avons plusieurs variables, XLSTAT va générer plusieurs visualisations pour nous permettre d'examiner les relations linéaires et les corrélations. Dans la matrice ci-dessous, nous voyons chaque variable comparée à chacune des autres variables. Il y a des tendances frappantes. 

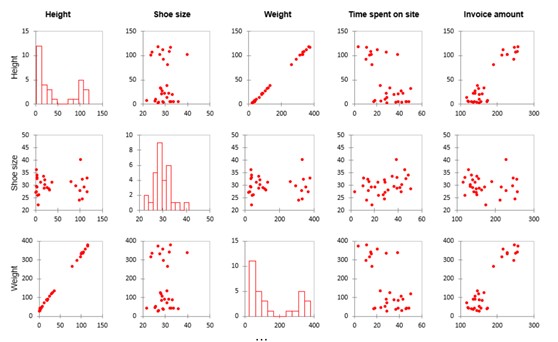
Remarquez les diagrammes de dispersion fortement linéaires dans les lignes de poids et de taille. Cela indique que ces variables présentent essentiellement les mêmes données (par exemple, la taille d'une personne). Nous appelons variables multicollinéaires les points de données qui mesurent le même facteur. Vous pouvez éliminer l'une ou l'autre de ces variables de votre modèle. Si vous ne le faites pas, les coefficients de votre modèle ne seront pas stables et les tests ne seront pas bons. C'est ce qu'on appelle un problème de multicolinéarité.  

Vous pouvez également générer une vérification de la multicollinéarité lors de l'exécution de la régression linéaire multiple dans XLSTAT en cliquant sur l'onglet « Sorties » et en cochant la case « Statistiques de multicollinéarité ». 

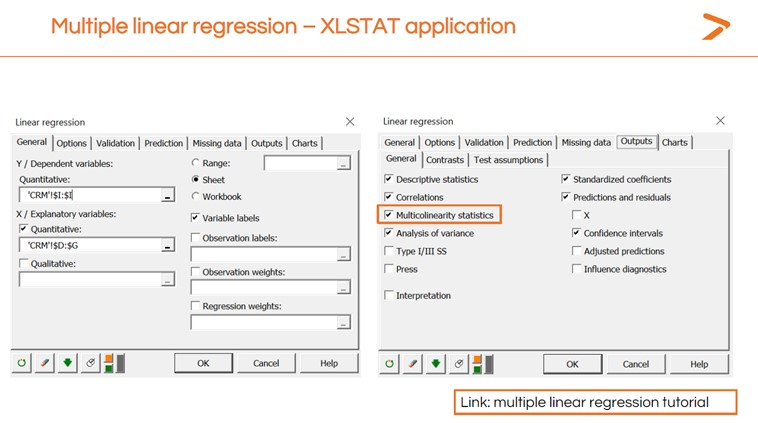
Les statistiques de multicolinéarité comprennent un facteur d'inflation de la variance (VIF) qui permet de déterminer le degré de redondance d'une variable explicative par rapport aux autres. Un chiffre élevé indique qu'il faut supprimer la variable redondante et relancer le MLR. 

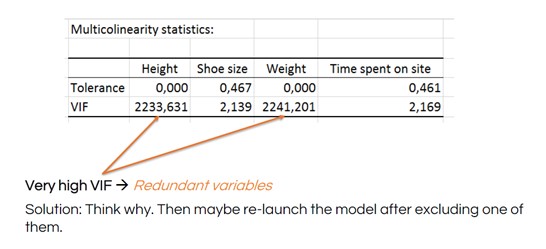
Voyez comment les chiffres de la VIF chutent après avoir retiré la hauteur du MLR : 

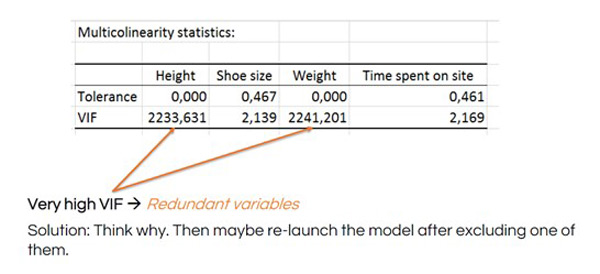
Après avoir exécuté votre MLR, vous voudrez vérifier les résidus comme vous l'avez fait pour la régression linéaire simple. Dans ce cas, le fait d'avoir plus de variables nous montre différents modèles dans les résidus qui pourraient indiquer d'autres techniques de modélisation statistique que nous pourrions essayer. 

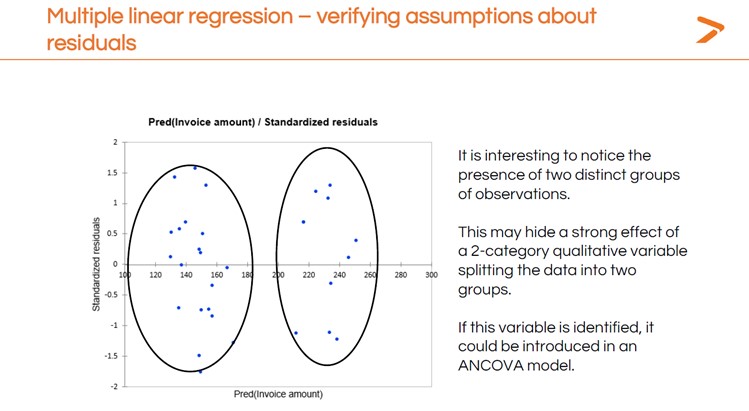
Vous voudrez également interpréter les résultats du MLR pour répondre à votre question : Quelle variable a le plus d'influence sur le montant de la facture ? 

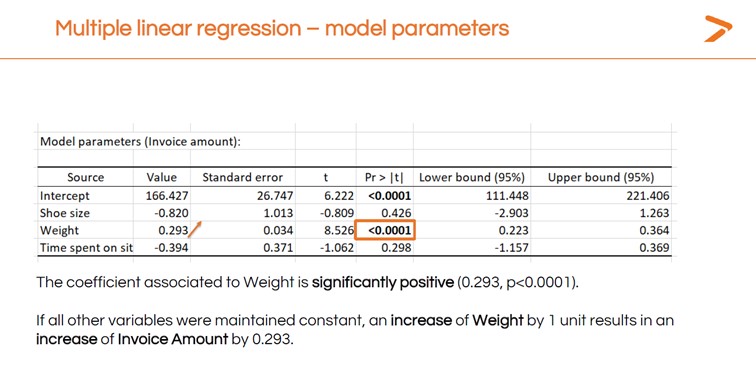
Les résultats de l'analyse de régression linéaire suggèrent que le poids est la seule variable ayant un impact positif fort et significatif sur le montant de la facture, puisqu'il s'agit de la seule variable ayant un test significatif. 

EN SAVOIR PLUS SUR LA RÉGRESSION LINÉAIRE SIMPLE ET MULTIPLE AVEC XLSTAT 

Vous souhaitez en savoir plus sur les puissants outils de modélisation statistique tels que l'analyse de régression que XLSTAT apporte à votre espace de travail Microsoft Excel ? Demandez une démonstration gratuite dès aujourd'hui. Vous pouvez également visiter la chaîne YouTube de XLSTAT pour plus de tutoriels vidéo.