Statistiques h et k de Mandel

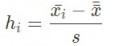
Qu'est-ce que les statistiques h et k de Mandel ?

Les statistiques h et k de Mandel (1985, 1991) ont été développées afin d'identifier dans le cadre d'analyses inter-laboratoires des laboratoires non conformes si des valeurs aberrantes (ou extrêmes) sont présentes au sein des échantillons. Ces statistiques permettent de rechercher des différences aux niveaux des échantillons, la statistique h au niveau de la moyenne et la statistique k au niveau de la variance.

Comment calculer la statistique de test h ?

La statistique h se calcule grâce à la formule suivante :

Avec x_i la moyenne du groupe i, x la moyenne globale, s l'écart-type global.

Cette statistique de test suit une loi de Student à p-2 degrés de liberté, p étant le nombre de groupes. Si elle prend des valeurs extrêmes, alors le groupe présente une moyenne significativement différente des autres, ce qui pourrait indiquer la présence de valeurs aberrantes.

Comment calculer la statistique de test k ?

La statistique de test k se calcule avec la formule suivante :

Elle suit une distribution de Fischer. Si elle prend des valeurs extrêmes, alors le groupe a une variance significativement des autres et cela y révèle la présence de valeurs aberrantes.

Valeurs extrêmes

On appelle valeur extrême (ou aberrante) une donnée observée pour une variable qui semble anormale au regard des valeurs dont on dispose pour les autres observations de l'échantillon. On distingue deux types de situations dans lesquelles on rencontre des valeurs extrêmes :

• Une valeur extrême peut indiquer une erreur de lecture, une erreur de saisie ou un événement particulier qui a perturbé le phénomène observé au point de le rendre incomparable aux autres. Dans de tels cas, il faut soit corriger la valeur extrême si c'est possible, soit supprimer l'observation.
• Une valeur extrême peut également être liée à un événement atypique, mais connu ou intéressant à étudier. Par exemple, si l'on étudie la présence de certaines bactéries dans de l'eau de rivière, on peut avoir des prélèvements sans aucune bactérie, et d'autres avec des agrégats importants ou très importants. Ces données sont bien entendu importantes à conserver. Les modèles utilisés doivent alors tenir compte de cette dispersion possible.

Lorsque l'on rencontre des valeurs extrêmes, en fonction du stade de l'étude, on doit, identifier les valeurs extrêmes, éventuellement à l'aide de tests, les marquer dans les rapports (tableaux ou graphiques), les supprimer ou utiliser des méthodes capables de les traiter comme tels.

Pour identifier les valeurs extrêmes, il existe différentes approches. Par exemple, en régression linéaire classique, on peut utiliser la valeur des D de Cook, ou soumettre les résidus standardisés au test de Grubbs afin de voir si une ou deux valeurs sont anormales. Le test de Grubbs simple permet d'identifier une valeur aberrante, le test de Grubbs double permet d'en identifier deux. Il est déconseillé d'utiliser itérativement ces méthodes sur un même échantillon, néanmoins cela peut être pertinent si l'on soupçonne réellement qu'il y a plus de deux valeurs extrêmes.

Lorsque l'échantillon peut être subdivisé en sous-échantillons, on peut s'intéresser aux variations d'un sous-échantillon à l'autre. Le test du C de Cochran et les statistiques h et k de Mandel font partie des méthodes adaptées à ce type d'études.

Références

International Organization for Standardization (1994). ISO 5725-2: Accuracy (trueness and precision) of measurement methods and results—Part 2: Basic method for the determination of repeatability and reproducibility of a standard measurement method, Geneva.

Mandel J. (1991). The validation of measurement through interlaboratory studies. Chemometrics and Intelligent Laboratory Systems; 11, 109-119.

Mandel J. (1985). A new analysis of interlaboratory test results. In: ASQC Quality Congress Transaction, Baltimore, 360-366.