Modèle logistique à quatre ou cinq paramètres

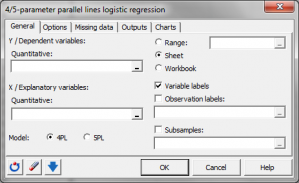
Le modèle logistique à quatre paramètres est donné par l'équation suivante :

y = a + (d -a) / [1 + (x / c)^b] modèle (1)

où a, b, c, d sont les paramètres du modèle, et x est la variable explicative, et y la variable réponse. Les paramètres a et d sont des paramètres d’asymptotes (a étant le minimum et d le maximum), et b est le paramètre de pente. Le paramètre c correspond à l’abscisse du point de mi-pente dont l’ordonnée est (a+b)/2. Lorsque a est inférieur à d, la courbe descend de d à a et, lorsque a est supérieur à d, la courbe monte de a à d.

Le modèle logistique à 5 paramètres est donné par l’équation suivante :

y = a + (d -a) / [1 + (x / c)^b]^e modèle (2)

Le paramètre e est un paramètre d’asymétrie.

Pour l’ajustement parallèle à 4 paramètres, le modèle utilisé est le suivant :
y = a + (d -a) / [1 + (st * x / c₁ + sp * x / c₂)^b] modèle (3)

où s0 vaut 1 si la donnée x provient de l’échantillon standard, et 0 sinon, et où s1 vaut 1 si la donnée x provient de l’échantillon étudié, et 0 sinon. Ce modèle est dit sous contrainte, car pour l’estimation des paramètres a, b, et d, les valeurs obtenues pour l’échantillon standard sont prises en compte. De la description des paramètres ci-dessus, on comprend que ce modèle génère deux courbes parallèles, dont la seule différence est la position, le décalage étant donné par (c2-c1). Si c2 est supérieur à c1, la courbe correspondant à l’échantillon étudié sera décalée à droite de la courbe correspondant à l’échantillon standard, et vice-versa.

Pour l’ajustement parallèle à 5 paramètres, le modèle utilisé est le suivant :

y = a + (d -a) / [1 + (st * x / c₁ + sp * x / c₂)^b]^e modèle (4)

XLSTAT permet d’ajuster :
•    Le modèle (1) ou (2), à un échantillon standard ou à un échantillon étudié,
•    Le modèle (3) ou (4), à la fois à l’échantillon standard et à l’échantillon étudié.

Si l’utilisateur le souhaite, XLSTAT-Dose peut tester pour chaque échantillon (standard et étudié) si des valeurs extrêmes perturbent l’ajustement. Pour les modèles (1) ou (2), le test de Dixon est appliqué une fois le modèle ajusté. Si une valeur anormale est détectée, elle est supprimée, et le modèle est recalculé, et ainsi de suite jusqu’à ce que plus aucune valeur extrême ne soit détectée. Pour les modèles (3) et (4), on effectue d’abord un test de Dixon avec les modèles (1) ou (2) sur l’échantillon standard, puis sur l’échantillon étudié, puis les modèles (3) ou (4) sont ajustés au regroupement des deux échantillons sans les observations supprimées.

Pour les modèles (3) ou (4) un test de Fisher est effectué afin de déterminer si les paramètres a, b et d (et éventuellement e) obtenus avec les modèles (1) ou (2) ne sont pas significativement différents pour les deux échantillons pris séparément.
 

Résultats de l’ajustement du modèle logistique à quatre paramètres

Si aucun groupe ou un seul échantillon a été sélectionné, les résultats sont affichés pour le modèle choisi et pour cet échantillon. Si plusieurs sous-échantillons ont été définis (option sous-échantillons dans la boîte de dialogue), le modèle est d’abord ajusté à l’échantillon standard, puis chaque sous-échantillon est comparé à l’échantillon standard.

Test de Fisher du parallélisme entre les courbes : le test de Fisher est utilisé pour déterminer si on peut considérer que l’échantillon standard et l’échantillon étudié ont des paramètres a, b, d et e (e n’est utilisé que si le modèle à 5 paramètre a été retenu) significativement identiques ou non. Si la probabilité associée à la valeur F obtenue est inférieure au seuil de signification que l’on se fixe (5% par exemple), alors on peut considérer que les deux échantillons ont des paramètres a, b, d et e significativement différents.

Coefficients d'ajustement : dans ce tableau sont affichées les statistiques suivantes :
•    le nombre d’observations ;
•    le nombre de degrés de liberté (DDL) ;
•    le coefficient de détermination R² ;
•    la somme des carrés des erreurs (ou résidus) du modèle (SCE) ;
•    la moyenne des carrés des erreurs (ou résidus) du modèle (MCE) ;
•    la racine de la moyenne des carrés des erreurs (ou résidus) du modèle (RMCE) ;

Paramètres du modèle : dans ce tableau sont affichés les estimateurs de chacun des paramètres du modèle, ainsi que l’écart-type correspondant.

Prédictions et résidus : ce tableau donne pour chaque observation, la valeur de la variable d’échantillon, les données de départ, la valeur prédite pour le modèle, les résidus. Si des observations ont été supprimées suite au test de Dixon, elles sont affichées en gras.

Graphiques : sur le premier graphique sont figurées en bleu les données et la courbe correspondant à l’échantillon standard, et en rouge les données et la courbe correspondant à l’échantillon étudié. Sur le deuxième graphique sont affichées les valeurs observées pour la variable dépendante en fonction des valeurs prédites. Le troisième graphique correspond au diagramme en bâtons des résidus.