Régression de Dirichlet

La régression de Dirichlet a pour but de prédire des données compositionnelles et s’utilise dans beaucoup de domaines tels que l’écologie, la santé et l’économie. Elle est disponible dans Excel via le logiciel XLSTAT.

À quoi sert la régression de Dirichlet ?

La régression de Dirichlet, comme la régression linéaire ou la régression logistique, a pour but de réaliser des prédictions en se basant sur une ou plusieurs variables explicatives. Cependant, contrairement à d’autres types de régression, la régression de Dircihlet ne prédit pas des valeurs précises d’une variable à expliquer mais plusieurs proportions dans le cadre de données compositionnelles. Ainsi, elle constitue une généralisation de la régression Bêta qui ne nous permet de prédire que deux proportions.

Dans quel contexte utiliser la régression de Dirichlet ?

Par exemple, si votre variable réponse est la proportion de différentes variétés d’arbres, vous pouvez prédire grâce à la régression de Dirichlet la proportion de chênes, pommiers ou bouleaux en vous basant sur des variables extérieures comme la température moyenne ou l’humidité dans chaque zone géographique concernée.

Comment marche la régression de Dirichlet dans XLSTAT ?

La fonction de régression de Dirichlet développée dans XLSTAT-R appelle la fonction DirichletReg du package R DirichletReg (développé par Macro Johannes Maier), qui propose plusieurs options afin que vous puissiez pleinement étudier vos données :

Sélectionnez plusieurs colonnes contenant les proportions à expliquer
Sélectionnez plusieurs variables explicatives
Incluez des interactions entre vos variables explicatives
Choisissez entre le modèle classique et le modèle alternatif
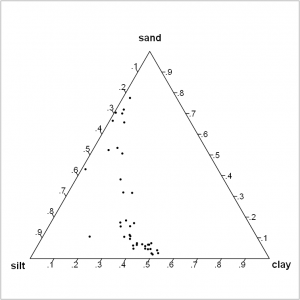
Visualisez la distribution de vos données avec un graphique ternaire

Quelle est la différence entre la régression de Dirichlet, la régression Bêta et la régression linéaire ?

Qu’est-ce que la régression linéaire ?

Contrairement à la régression de Dirichlet et à la régression Bêta, la régression linéaire ne prédit pas des proportions. Elle consiste à prédire une variable quantitative basée sur une ou plusieurs autres variables quantitatives et suppose qu’une relation linéaire existe entre les variables. Voici l’équation d’un modèle de régression linéaire :

Y=X*β + ε

avec Y le vecteur des valeurs des variables prédites, X le vecteur (ou matrice) des valeurs des variables explicatives, β le vecteur des coefficients de régression et ε l’erreur aléatoire. Si vous désirez en savoir plus sur la régression linéaire dans XLSTAT, n’hésitez pas à consulter la page correspondante.

Qu’est-ce que la régression Bêta ?

La régression Bêta est utilisée pour prédire la probabilité qu’un évènement (et son opposé) se produise. Elle suppose que la variable réponse suit une loi Bêta: Y ~ B(μ,φ) avec mu la moyenne et phi un paramètre de précision tel que p=mu*φ est un paramètre de forme. Nous devons estimer ces paramètres à l’aide de nos données. Pour ce faire, nous utilisons pour chaque variable y_t une fonction de lien telle que g(μ_t)=X*β+ε et nous appliquons la méthode de régression linéaire mentionnée ci-dessus afin d’identifier les valeurs g(μ_t) qui nous permettent ensuite d’estimer chaque μ_t et φ avant de trouver le paramètre de forme p.

Vous souhaitez savoir quand utiliser la régression Bêta ? Par exemple, supposons que nous voulons prédire la probabilité pour chaque habitant français d’être en bonne ou en mauvaise santé en nous basant sur des facteurs comme le tabagisme, la consommation d’alcool et le nombre d’heures de sommeil moyen par nuit. Dans ce cas, l’évènement serait “sain” et son opposé “malade”, puis nous estimerions la probabilité que la personne soit en bonne santé.

Qu’est-ce que la régression de Dirichlet ?

Et la régression de Dirichlet ? La régression de Dirichlet est une généralisation de la régression Bêta. Au lieu de prédire une seule probabilité ou proportion, elle peut prédire plusieurs proportions ou probabilités pour plus de deux issues par une approche similaire. Nous supposons que la variable réponse suit une loi de Dirichlet, comparable à la loi Bêta mais considère plus d’un évènement ainsi que son opposé.

Elle peut être utilisée comme dans l’exemple précédent pour prédire des proportions d’espèces différentes. Cependant, nous pouvons également étendre l’exemple de la régression Bêta à une échelle de santé de 1 à 5 au lieu de simplement “sain” ou “malade”.