Tests auf Heteroskedastizität
Das Konzept der Heteroskedastizität – ihr Gegensatz ist die Homoskedastizität – kommt in der Statistik, insbesondere im Zusammenhang mit linearer Regression oder Zeitreihenanalyse, bei der Beschreibung von Fällen zur Anwendung, in denen die Fehlervarianz oder das Modell nicht für alle Beobachtungen gleich ist, während eine der Grundannahmen der Modellierung häufig gerade darin liegt, dass die Varianzen homogen und die Fehler des Modells identisch verteilt sind.
Wenn bei der linearen Regressionsanalyse die Fehler des Modells (auch als Residuen bezeichnet) nicht homoskedastisch sind, so folgt daraus, dass die anhand der Methode der kleinsten Quadrate (Ordinary Least Squares, OLS) geschätzten Koeffizienten des Modells nicht erwartungstreu sind noch über die kleinstmögliche Varianz verfügen. Die Schätzung der Varianzen ist somit unzuverlässig.
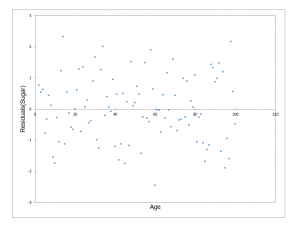
Wenn die Vermutung besteht, dass die Varianzen nicht homogen sind (eine Darstellung der Residuen im Vergleich zu den erklärenden Variablen kann Heteroskedastizität ausdrücken), ist daher die Durchführung eines Tests auf Heteroskedastizität erforderlich. Mehrere Tests mit folgenden Null- und Alternativhypothesen wurden entwickelt:
- H0: Die Residuen sind homoskedastisch
- Ha: Die Residuen sind heteroskedastisch
In XLSTAT sind jetzt enthalten:
- Breusch-Pagan-Test
- White-Test und modifizierter White-Test (Wooldridge)


analysieren sie ihre daten mit xlstat
Enthalten ind
Verwandte Funktionen