Análisis de un diseño de mezclas

¿Qué es un análisis de diseño de mezclas?

Descripción de modelos

El análisis de un diseño de mezclas se basa en el mismo principio de una regresión lineal. La mayor diferencia es el modelo usado. Varios modelos están disponibles.

De forma predeterminada, XLSTAT asocia un modelo reducido (modelo canónico simplificado) a centroides símplex. Sin embargo, es posible cambiar el modelo si el número de grados de libertad es suficiente (aumentando el número de repeticiones de los experimentos).

Para cumplir con la restricción asociada a un diseño de mezclas, se usa un modelo polinomial sin intercepto. Distinguimos dos tipos de modelos, modelos simplificados (especiales) y modelos completos (a partir del nivel 3).

Están disponibles los siguientes modelos:

• Modelo lineal (nivel 1)
• Modelo cuadrático (nivel 2)
• Modelo cúbico completo (nivel 3)
• Modelo cúbico simplificado (especial)
• XLSTAT permite aplicar modelos hasta el nivel 4 (modelo cuartico simplificado y completo).

La estimación de estos modelos se realiza como en la regresión clásica.

Respuestas optimizadas y deseables

En el caso de muchos valores respuesta y1, ..., ym, es posible optimizar cada valor respuesta individualmente y crear una función de deseabilidad combinada y analizar sus valores. Propuesto por Derringer y Suich (1980), este enfoque consiste en convertir primero cada respuesta yi en una función de deseabilidad individual di que varía en el rango 0 ≤ di ≤ 1.

En la pantalla, XLSTAT ofrece las 5 mejores soluciones encontradas durante la optimización.

Resultados del análisis de diseño mixto en XLSTAT

Información de variables: esta tabla muestra la información sobre los factores. Para cada factor, se muestran el nombre corto, el nombre largo, la unidad y la unidad física.

Optimización de respuestas: esta tabla muestra las 5 mejores soluciones obtenidas durante la optimización de respuestas.

Matriz de correlación: esta tabla muestra las correlaciones entre las diversas variables seleccionadas.

Estadísticos de bondad de ajuste: Los estadísticos relacionados con el ajuste del modelo de regresión se muestran en esta tabla (número de observaciones, suma de ponderaciones, DF, R2, R2 ajustado, MSE, RMSE, MAPE, el estadístico de Durbin-Watson (DW) , Coeficiente Cp de malvas (Cp), AIC, Bayesiano de Schwarz (SBC), Criterio de predicción de Amemiya (PC), Estadística de Press, Q2).

La tabla del análisis de varianza se utiliza para evaluar el poder explicativo de las variables explicativas.

La tabla de parámetros del modelo muestra la estimación de los parámetros, el error estándar correspondiente, la prueba t-Student, la probabilidad correspondiente, así como el intervalo de confianza.

La ecuación del modelo para facilitar la lectura o la reutilización del modelo.

La tabla de coeficientes estandarizados (también llamados coeficientes beta) se utiliza para comparar los pesos relativos de las variables. Cuanto mayor sea el valor absoluto de un coeficiente, más importante será la ponderación de la variable correspondiente. Cuando el intervalo de confianza alrededor de los coeficientes estandarizados tiene valor 0 (esto se puede ver fácilmente en el gráfico de coeficientes estandarizados), el peso de una variable en el modelo no es significativo.

La tabla de predicciones y residuales muestra para cada observación, su ponderación, el valor de la variable explicativa cualitativa, si hay una sola, el valor observado de la variable dependiente, la predicción del modelo, los residuales, los intervalos de confianza junto con el ajustado. predicción y la D de Cook si se han activado las opciones correspondientes en el cuadro de diálogo.

Los gráficos que siguen muestran los resultados mencionados anteriormente. Si solo hay una variable explicativa en el modelo, el primer gráfico muestra los valores observados, la línea de la regresión y ambos tipos de intervalo de confianza alrededor de las predicciones. El segundo gráfico muestra los residuos estandarizados en función de la variable explicativa. En principio, los residuos deben distribuirse aleatoriamente alrededor del eje X. Si hay una tendencia o una forma, esto muestra un problema con el modelo.

Los tres gráficos a continuación muestran respectivamente la evolución de los residuos estandarizados como una función de la variable dependiente, la distancia entre las predicciones y las observaciones (para un modelo ideal, los puntos estarían todos en la bisectriz) y los residuos estandarizados en un gráfico de barras. El último gráfico muestra rápidamente si un número anormal de valores está fuera del intervalo [-2, 2] dado que este último, suponiendo que la muestra se distribuye normal, debería contener alrededor del 95% de los datos.

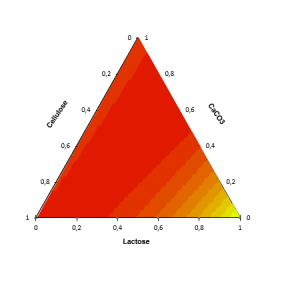
Para cada combinación de los factores, dibujamos un diagrama ternario. Este gráfico muestra una superficie respuesta en una de las caras del poliedro al que corresponde el espacio experimental. Estos gráficos facilitan la interpretación del modelo y permiten identificar las configuraciones óptimas.