Los estadísticos h y k de Mandel para los valores atípicos

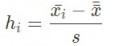
¿Qué son los estadísticos h y k de Mandel?

Los estadísticos h y k de Mandel (1985, 1991) se han desarrollado para ayudar a identificar los valores atípicos durante los estudios entre laboratorios. La idea de estos estadísticos es detectar las diferencias entre las muestras obtenidas en diferentes laboratorios para ver si una muestra contiene valores atípicos en comparación con otras. El estadístico h detecta la diferencia entre medias y el estadístico k detecta la diferencia entre varianzas.

¿Cómo se calcula el estadístico h?

El estadístico h se calcula con la siguiente fórmula para la muestra i:

con x_i la media en la muestra i, s la varianza intergrupal y x la media global.

Sigue una distribución de Student con p-2 grados de libertad, siendo p el número de grupos. Si toma valores extremos, entonces el grupo tiene una media significativamente diferente a la de los demás grupos, lo que podría mostrar la presencia de valores atípicos en él.

¿Cómo se calcula el estadístico k?

El estadístico k se calcula con la siguiente fórmula:

Sigue una distribución de Fisher. Si toma valores extremos, entonces el grupo tiene una varianza significativamente diferente de los otros grupos, lo que podría mostrar la presencia de valores atípicos en él.

Detección de valores atípicos

En estadística, un valor atípico es un valor registrado para una determinada variable, que parece inusual y sospechosamente menor o mayor que los demás valores observados. Se pueden distinguir dos tipos de valores atípicos:

• Un valor atípico puede estar relacionado simplemente con un error de lectura (en un instrumento de medida), un error de teclado o un acontecimiento especial que haya perturbado el fenómeno observado hasta el punto de hacerlo incomparable con otros. En estos casos, hay que corregir el valor atípico, si es posible, o bien eliminar la observación para evitar que perturbe los análisis previstos (análisis descriptivo, modelización, predicción).
• Un valor atípico también puede deberse a un acontecimiento atípico, pero conocido o interesante de estudiar. Por ejemplo, si estudiamos la presencia de determinadas bacterias en el agua de un río, puede haber muestras sin bacterias y otras con agregados con muchas bacterias. Por supuesto, es importante conservar estos datos. Los modelos utilizados deben reflejar esa posible dispersión.

Cuando hay valores atípicos en los datos, dependiendo de la fase del estudio, debemos identificarlos, posiblemente con ayuda de pruebas, marcarlos en los informes (en tablas o en representaciones gráficas), eliminarlos o utilizar métodos capaces de tratarlos como tales.

Para identificar los valores atípicos, existen diferentes enfoques. Por ejemplo, en la regresión lineal clásica, podemos utilizar el valor de la d de Cook, o someter los residuos estandarizados a una prueba de Grubbs para ver si uno o dos valores son anómalos. La prueba de Grubbs clásica puede ayudar a identificar un valor anómalo, mientras que la prueba de Grubbs doble permite identificar dos. No se recomienda utilizar estos métodos repetidamente en la misma muestra. Sin embargo, puede ser apropiado si realmente se sospecha que hay más de dos valores atípicos.

Si la muestra puede dividirse en submuestras, podemos buscar cambios de una submuestra a otra. La prueba C de Cochran y los estadísticos h y k de Mandel forman parte de los métodos adecuados para este tipo de estudios.

Referencias

Barnett V. and Lewis T. (1980). Outliers in Statistical Data. John Wiley and Sons, Chichester, New York, Brisbane, Toronto.

Hawkins D.M. (1980). Identification of Outliers. Chapman and Hall, London.

International Organization for Standardization (1994). ISO 5725-2: Accuracy (trueness and precision) of measurement methods and results—Part 2: Basic method for the determination of repeatability and reproducibility of a standard measurement method, Geneva.

Mandel J. (1991). The validation of measurement through interlaboratory studies. Chemometrics and Intelligent Laboratory Systems; 11, 109-119.

Mandel J. (1985). A new analysis of interlaboratory test results. In: ASQC Quality Congress Transaction, Baltimore, 360-366.

Wilrich P.-T. (2013). Critical values of Mandel’s h and k, the Grubbs and the Cochran test statistic. Advances in Statistical Analysis, 97(1), 1-10.