Pruebas de heterocedasticidad

¿Qué es la heteroscedasticidad?

El concepto de heteroscedasticidad -su opuesto es la homocedasticidad- se utiliza en estadística, especialmente en el contexto de la regresión lineal o para el análisis de series temporales. Sirve para describir el caso en que la varianza de los errores del modelo no es la misma para todas las observaciones, mientras que a menudo uno de los supuestos básicos en la modelización es que las varianzas son homogéneas y que los errores del modelo se distribuyen de forma idéntica.

¿Por qué es un problema la heteroscedasticidad?

En el análisis de regresión lineal, el hecho de que los errores del modelo (también denominados residuos) no sean homocedásticos tiene como consecuencia que los coeficientes del modelo estimados mediante mínimos cuadrados ordinarios (MCO) no sean insesgados ni tengan una varianza mínima. La estimación de su varianza no es fiable.

Cómo comprobar la heteroscedasticidad en XLSTAT

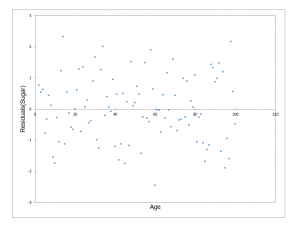
Si se sospecha que las varianzas no son homogéneas (una representación de los residuos frente a las variables explicativas puede revelar heteroscedasticidad), es necesario realizar una prueba de heteroscedasticidad. Se han desarrollado varias pruebas, con las siguientes hipótesis nulas y alternativas:

H0 : Los residuos son homocedasticos Ha : Los residuos son heteroscedásticos

Prueba de Breusch-Pagan

Este test de heteroscedasticidad ha sido desarrollado por Breusch y Pagan (1979), y posteriormente mejorado por Koenker (1981) -por lo que este test se denomina a veces test de Breusch-Pagan y Koenker- para permitir identificar los casos de heteroscedasticidad, que hacen que los estimadores clásicos de los parámetros de la regresión lineal no sean fiables. Si e es el vector de los errores del modelo, la hipótesis nula H0 de que dichos términos de error son de varianza constante puede escribirse

H0 : E(e2) = σ2

Para verificar que los errores cuadráticos son independientes de las variables explicativas, lo que puede traducirse en muchas formas funcionales, lo más sencillo es hacer una regresión de los errores al cuadrado por las variables explicativas. Si los datos son homoscedásticos, el coeficiente de determinación R2 no debería ser igual a 0. Si no se rechaza H0, podemos concluir que la heteroscedasticidad, si existe, no adopta la forma funcional utilizada. La práctica demuestra que la heteroscedasticidad no es un problema si no se acepta H0. Si se rechaza H0, es probable que haya heteroscedasticidad y que ésta adopte la forma funcional descrita anteriormente.

El estadístico utilizado para la prueba, propuesto por Koenker (1981) es

LM = nR2

donde LM significa multiplicador de Lagrange. Este estadístico tiene la ventaja de seguir asintóticamente una distribución Chi-cuadrado con p grados de libertad, donde p es el número de variables explicativas.

Si se rechaza la hipótesis nula, será necesario transformar los datos antes de hacer la regresión, o utilizar métodos de modelización para tener en cuenta la variabilidad de la varianza.

Prueba de White y prueba de White modificada (Wooldridge)

¿Cómo se detecta la heteroscedasticidad mediante el test de White? Esta prueba fue desarrollada por White (1980) para identificar los casos de heteroscedasticidad que hacen que los estimadores clásicos de los parámetros de la regresión lineal no sean fiables. La idea es similar a la de Breusch y Pagan, pero se basa en supuestos más débiles en cuanto a la forma que adopta la heteroscedasticidad. El resultado es una regresión de los errores cuadráticos por las variables explicativas y por los cuadrados y productos cruzados de estas últimas. Se utiliza el mismo estadístico que para el test-Breusch Pagan, pero debido a la presencia de muchos más regresores, aquí hay 2p+p*(p-1)/2 grados de libertad para la distribución Chi-cuadrado.

Para evitar perder demasiados grados de libertad, Wooldrigde (2009) propuso hacer una regresión de los errores al cuadrado por las predicciones del modelo y por su cuadrado. Esto reduce a 2 el número de grados de libertad para la Chi-cuadrado.

Cómo corregir la heteroscedasticidad en XLSTAT

Newey West y otros estimadores

XLSTAT permite aplicar correcciones de heteroscedasticidad. Hay varios estimadores (Newey West, HC0, HC1, etc.) disponibles para este fin en la herramienta de regresión lineal.

White (1980), seguido por varios autores, ha explorado formas de corregir la estimación clásica de las covarianzas usando los residuos y los apalancamientos centrados obtenidos de los cálculos de regresión lineal (véase MacKinnon (1985) y Zeileis (2006) para una revisión). Cuando los supuestos de la regresión lineal clásica no se cumplen, mientras que los estimadores de los coeficientes no cambian, la escritura simplificada de la matriz de covarianza de los parámetros beta no es posible, y debemos volver a la expresión general

Var (β) = (XtX)-1 (Xt ΩX)(XtX)-1

Transformación de la variable dependiente

Puede utilizar la herramienta de transformación de variables de XLSTAT para aplicar una transformación de Box-Cox con el fin de corregir la heteroscedasticidad.

Regresión ponderada

También puede ajustar una regresión ponderada para tratar la heteroscedasticidad. Cada modelo de regresión en XLSTAT nos permite seleccionar los pesos a través de su cuadro de diálogo.

Resultados de las pruebas de heteroscedasticidad en XLSTAT

La salida incluye:

• una tabla de resumen estadístico
• un gráfico de residuos
• los resultados de las pruebas seleccionadas (estadística de la prueba, valor crítico, valor p, alfa)

Tutorial sobre las pruebas de heteroscedasticidad

¿Se pregunta cómo realizar una prueba de heteroscedasticidad en Excel? Lea cómo configurar e interpretar una prueba de heteroscedasticidad en Excel utilizando el software XLSTAT.