Modèle Illness-Death paramétrique

Utilisez le modèle Illness-Death afin de déterminer le temps de survie et de modéliser les différents états parcourus au cours du temps. Disponible dans Excel avec le logiciel XLSTAT.

Description d'un modèle Illness-Death paramétrique dans XLSTAT

Lorsque l'on dénombre plus de 2 états en survie, on parle alors de modèle multi-états. Le modèle Illness-Death est un modèle multi-états particulier qui fait intervenir 3 états : l'état initial, l'état transitoire et l'état absorbant notés respectivement 0, 1, 2.

Ce modèle est largement utilisé en épidémiologie pour observer l'évolution d'une maladie, l'influence d'une maladie sur la mortalité ou encore de la mortalité post-opératoire. On retrouve aussi de nombreuses applications dans le domaine actuarial pour calculer les coûts d'assurances et des contrats viatiques.

Censures et troncatures

En analyse de survie les censures et troncatures représentent un manque d'information lors du recueil des données. Si l'on les ignore, les estimations seront faussées. Le modèle Illness-Death de XLSTAT accepte les censures à droite et par intervalle ainsi que les troncatures à gauche sous l'hypothèse que les censures et troncatures sont non-informatives.

Les censures interviennent lorsque l'on ne connait pas la date exacte de survenue de l'événement tandis que les troncatures interviennent lorsque l'événement ne peut pas se produire avant ou après un seuil donné.

La censure à droite se produit lorsque le sujet n'a pas subi l'événement absorbant à la fin de sa période d'observation. En d'autres mots, si on considère t le temps de la survenue de l'événement et tfin le temps de fin d'observation alors t > tfin
La censure par intervalle se produit lorsque le sujet subit l'événement entre deux observations. En d'autres mots, si on considère tl et tl+1 les temps de deux visites consécutives alors la survenue de l'événement au temps t s'est produite telle que t ∈ [tl , tl+1]
La troncature à gauche se produit lorsque l'individu ne peut pas subir l'événement avant le début de l'étude.

Algorithme de Levenberg-Marquardt (LM)

L’estimation des intensités de transition du modèle Illness-Death se fait en maximisant la log-vraisemblance avec l’algorithme de Levenberg-Marquardt.

Cette procédure itérative associe deux méthodes d’optimisation :

La méthode de descente du gradient : maximise la log-vraisemblance et met à jour les paramètres à chaque itération dans la direction du gradient.
La méthode de Newton-Raphson : maximise la dérivée de la log-vraisemblance et met à jour les paramètres à chaque itération.

Lors de l’optimisation, l’algorithme agit comme la méthode de descente du gradient lorsque les paramètres sont loin de la solution et comme la méthode de Newton-Raphson lorsque les paramètres sont proches de la solution. Ainsi, l'algorithme de LM est plus rapide que la méthode du gradient, longue à converger, et plus efficace que la méthode de Newton, coûteuse en temps de calcul.

Prédictions : Probabilités de transition et espérances de vie

Les prédictions permettent à l'utilisateur de donner les probabilités de transition et l'espérance de vie des individus entre 2 temps :

le temps d'entrée dans l'étude,
le temps de sortie de l'étude.

Parmi les probabilités de transition, on a :

p00 la probabilité de rester dans l'état initial,
p01 la probabilité de passer de l'état initial à l'état transitoire,
p02 la probabilité de passer de l'état initial à l'état absorbant,
p11 la probabilité de rester dans l'état transitoire,
p12 la probabilité de passer de l'état transitoire à l'état absorbant.

Parmi les espérances de vie, on a :

E00 l'espérance de vie non-malade : c'est à dire le temps que l'on peut espérer pour un individu de rester dans l'état initial sachant qu'il y est déjà,
E02 l'espérance de vie au sens commun : c'est à dire le temps que l'on peut espérer pour un individu de vivre sachant qu'il est dans l'état initial,
E12 l'espérance de vie d'un individu malade : c'est à dire le temps qu'on peut espérer pour un individu de vivre sachant qu'il est dans l'état transitoire.

Les formules explicites de ces probabilités et espérances de vie sont données dans les travaux de Touraine C. (2013).

Résultats d'un modèle Illness-Death paramétrique dans XLSTAT

XLSTAT propose un nombre important de tableaux et de graphiques afin de faciliter l'analyse et l'interprétation des résultats.

Statistiques descriptives : le tableau des statistiques descriptives présente pour les indicateurs d'états et les données de temps des statistiques simples. Pour les temps, sont affichés le nombre d'observations, le nombre de données manquantes, le nombre de données non-manquantes, la moyenne, et l'écart-type (non biaisé). Pour les indicateurs d'états, sont affichées les modalités, leurs effectifs et pourcentages respectifs.

Coefficients de régression et Paramètres de Weibull : ces tableaux affichent les paramètres de Weibull et de régression. Les paramètres de Weibull permettent de calculer les intensités de base. Si le modèle inclut des variables, alors pour chaque variable sont affichés l'estimation du coefficient de régression, l'écart-type correspondant, le χ2 de Wald, la p-value correspondante. Par ailleurs, le Hazard Ratio (exponentielle du coefficient) est donné ainsi qu'un intervalle de confiance associé.

Intensités de transition : ce tableau affiche les intensités de transition qui sont les pendants de la fonction de risque d’un modèle de survie. Observer les intensités de transition permet de comparer les risques de transition entre états.

Probabilités de transition : ce tableau affiche les probabilités de transition. Observer les probabilités de transition permet de comparer les transitions entre états. Ces quantités sont plus facilement interprétables et plus intuitives que les intensités de transition.

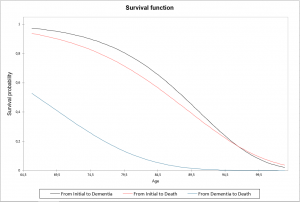
Fonctions de survie : ce tableau affiche les fonctions de survie. Observer les fonctions de survie permet de voir la probabilité de quitter un état. Ces quantités sont plus facilement interprétables et plus intuitives que les intensités de transition.

Prédictions : ce tableau affiche les probabilités de transition prédites et les 3 espérances de vie : au sens commun, de rester malade (rester dans l'état transitoire) et de rester sain (rester dans l'état initial). Les prédictions sont calculées en fonction du temps d'entrée et du temps de sortie de l'étude indiqués par l'utilisateur. Si des variables explicatives ont été ajoutées lors de la prédiction alors les résultats sont donnés pour chaque individu dont on a rentré les covariables associées, sinon les résultats correspondent à un seul individu.