ANOVA (Analisis de la varianza)

Utilice este modelo para llevar a cabo el ANOVA (Análisis de la varianza) de uno o más factores equilibrados o desequilibrados. Disponible en Excel con el software XLSTAT.

Utilice este modelo para realizar un ANOVA (Análisis de la varianza) con uno o más factores equilibrados o desequilibrados. Disponible en Excel con el software XLSTAT.

Principios del análisis de la varianza

El análisis de la varianza (ANOVA) es una herramienta que se usa para dividir la varianza observada en una variable concreta en componentes atribuibles a diferentes fuentes de variación.

El análisis de la varianza (ANOVA) utiliza el mismo marco conceptual que la regresión lineal. La principal diferencia proviene del tipo de las variables explicativas: en lugar de cuantitativas, aquí son cualitativas. En el ANOVA, las variables explicativas suelen denominarse factores.

Dependiendo del número de factores, se puede realizar una prueba de ANOVA de un factor, pero también un ANOVA de dos factores o incluso un ANOVA de medidas repetidas. Un ANOVA de un factor tiene una variable explicativa, mientras que un ANOVA de dos factores tiene dos, y así sucesivamente. En todos los casos, la hipótesis nula del ANOVA es que la varianza de la variable dependiente no varía en función de las modalidades de los factores.

Si no se puede aceptar la hipótesis nula, podemos concluir que los factores influyen significativamente en los valores de la variable dependiente.

¿No está seguro de si el ANOVA se adapta a sus datos? ¿Todavía se pregunta cuándo utilizar un ANOVA? Consulte nuestra guía para elegir la herramienta de modelización adecuada según su situación.

¿Qué es un modelo ANOVA?

Si p es el número de factores, el modelo ANOVA se escribe así:

y_i = β₀ + ∑_j=1...p β_{k_(i,j),j} + ε_i

donde yi es el valor observado de la variable dependiente para la observación i, k(i,j) es el índice de la categoría (o nivel) del factor j para la observación i y εi es el error del modelo.

El siguiente gráfico muestra datos que podrían analizarse mediante un ANOVA de un factor. El factor tiene tres categorías. Los datos se representan aquí con puntos naranjas. La línea verde discontinua es la media general y las líneas verdes cortas son las medias de las categorías. Observe que utilizamos arbitrariamente la restricción suma(ai)=0, lo que significa que β₀ corresponde a la media general.

Tenemos que verificar dos hipótesis principales en el ANOVA. Las hipótesis utilizadas en el ANOVA son idénticas a las utilizadas en la regresión lineal: los errores εif siguen la misma distribución normal N(0,s) y son independientes. Se recomienda comprobar a posteriori que las hipótesis subyacentes han sido comprobadas correctamente. Es posible verificar la hipótesis de normalidad mediante el análisis de ciertos gráficos sobre los residuos o mediante una prueba de normalidad. La independencia de los residuos puede comprobarse analizando determinados gráficos o utilizando la prueba de Durbin Watson.

Selección de datos en XLSTAT

Normalmente, para ejecutar un análisis en XLSTAT, es necesario que cada columna corresponda a una sola variable.

Sin embargo, la herramienta ANOVA de XLSTAT le permite seleccionar los datos de dos maneras diferentes cuando tiene hasta tres factores (variables explicativas):

Seleccione una sola columna de valores para cada variable (dependiente y factores).
Seleccionar una tabla de datos agrupados en la que las filas categorizan los datos según un factor, y las columnas los categorizan según los otros factores.

Opciones para configurar un ANOVA en XLSTAT

XLSTAT le permite realizar ANOVA de uno y multiples factores. Pueden incluirse en el modelo interacciones hasta el orden 4, así como efectos anidados y aleatorios.
XLSTAT puede realizar ANOVA balanceados y no balanceados.
XLSTAT tiene un dispositivo automático para encontrar factores anidados y un factor anidado puede ser incluido en el modelo.
Se pueden incluir factores aleatorios en un análisis ANOVA. Cuando se supone que algunos factores son aleatorios, XLSTAT muestra la tabla de cuadrados medios esperados.
Se proponen cuatro métodos para la selección del modelo: Mejor modelo, Stepwise, Forward, Backward
Supuestos de prueba: se realiza una prueba de Shapiro-Wilk sobre los residuos. Se dispone de una prueba de Levene para realizar una prueba sobre la homogeneidad de las varianzas. La prueba se realiza para comparar cada factor y la varianza de las diferentes categorías.

Cuando no se cumplen las condiciones del ANOVA: ¿cómo comprobar los supuestos del ANOVA?

XLSTAT permite corregir la heteroscedasticidad y la autocorrelación que pueden surgir utilizando varios métodos, como el estimador sugerido por Newey y West (1987).

La homocedasticidad y la independencia de los términos de error son hipótesis clave en la regresión lineal y en el ANOVA, donde se supone que las varianzas de los términos de error son independientes, idénticamente distribuidas y siguen una distribución normal. Cuando estos supuestos no se pueden mantener (una prueba de Durbin Watson o White disponible en el menú de series temporales permite desafiar estas hipótesis), una consecuencia es que la matriz de covarianza no se puede estimar utilizando la fórmula clásica. Entonces, la varianza de los parámetros correspondientes a los coeficientes del modelo lineal puede ser errónea y sus intervalos de confianza también. Se podría decir que un predictor es significativo (o respectivamente no) siendo lo contrario. XLSTAT permite corregir la heteroscedasticidad y la autocorrelación que pueden surgir, especialmente en las series temporales.

En lo que respecta a la heteroscedasticidad, White (1980), seguido de varios autores, ha explorado formas de corregir la estimación clásica de las covarianzas utilizando los residuos y los apalancamientos centrados obtenidos de los cálculos de regresión lineal (MacKinnon (1985) y Zeileis (2006)).

Pruebas de comparaciones múltiples tras el ANOVA

Una de las principales aplicaciones del ANOVA son las pruebas de comparación múltiple, cuyo objetivo es comprobar si los parámetros de las distintas categorías de un factor difieren significativamente o no. Por ejemplo, en el caso de que se apliquen cuatro tratamientos a las plantas, queremos saber no solo si los tratamientos tienen un efecto significativo, sino también si los tratamientos tienen efectos diferentes.

Se han propuesto numerosas pruebas para comparar las medias de los grupos. La mayoría de estas pruebas suponen que la muestra está distribuida normalmente.

Resultados del análisis de la varianza en XLSTAT

Los resultados contienen un análisis de residuos, los parámetros de los modelos, la ecuación del modelo, los coeficientes estandarizados, la SS de tipo I, la SS de tipo III y las predicciones.

Además, se pueden realizar opcionalmente varios métodos de comparaciónes múltiples, también llamados pruebas post-hoc: La prueba t corregida de Bonferroni y Dunn-Sidak, la prueba HSD de Tukey, la prueba LSD de Fisher, la prueba de Duncan, el método de Newman-Keuls (SNK) y el método REGWQ. Además, la prueba de Dunnett está disponible para permitir a los usuarios realizar comparaciones múltiples con una categoria de control (MCC) y comparaciones múltiples con el mejor (MCB). La prueba de Games-Howell (GH) puede utilizarse en ANOVAs de un factor cuando las varianzas carecen de homogeneidad. Aunque puede utilizarse con tamaños de muestra desiguales, se recomienda utilizarla cuando la muestra más pequeña tiene 5 elementos o más, ya que, de lo contrario, es demasiado liberal.

Además, se muestran diagnósticos de influencia para cada observación, incluyendo el residuo, el residuo estandarizado (dividido por el RMSE), el residuo estudiado, el residuo eliminado, el residuo eliminado estudiado, el apalancamiento, la distancia de Mahalanobis, la D de Cook, el CovRatio, el DFFit, el DFFit estandarizado, el DFBetas (uno por coeficiente del modelo) y el DFBetas estandarizado.

Algunos gráficos propuestos en el análisis de la varianza en XLSTAT

Gráfico de coeficientes estandarizados: El gráfico de barras muestra los valores e intervalos de confianza de los coeficientes estandarizados.

Gráfico de regresión: El gráfico muestra los valores observados, la línea de regresión y ambos tipos de intervalo de confianza en torno a las predicciones.
Residuos estandarizados en función de las predicciones del modelo: En principio, los residuos deberían distribuirse aleatoriamente alrededor del eje X. Si hay una tendencia o una forma, esto muestra un problema con el modelo.

Distancia entre las predicciones y las observaciones: Para un modelo ideal, los puntos estarían todos en la bisectriz.
Residuos estandarizados en un gráfico de barras: El último gráfico muestra rápidamente si un número anormal de valores está fuera del intervalo]-2, 2[ dado que este último, suponiendo que la muestra se distribuye normalmente, debería contener alrededor del 95% de los datos.

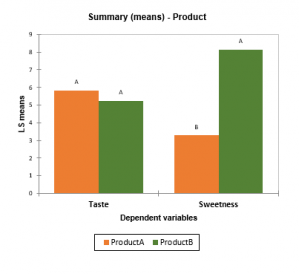
Gráficos de resumen: Si se han seleccionado varias variables dependientes y si se ha activado la opción de comparaciones múltiples, un gráfico permite visualizar las medias estimadas con letras de agrupación de comparaciones múltiples.