Regresión lineal

¿Qué es el análisis de regresión lineal?

La regresión lineal es, sin duda, uno de los métodos de modelización estadística los más utilizados. Se suele distinguir entre regresión simple (con una sola variable explicativa) y regresión múltiple (varias variables explicativas), aunque el concepto general y los métodos de cálculo son idénticos.

El principio de la regresión lineal consiste en modelizar una variable dependiente cuantitativa Y mediante una combinación lineal de p variables explicativas cuantitativas, X1, X2, ..., Xp. La ecuación de regresión lineal se escribe para la observación i como sigue

donde y_i es el valor observado de la variable dependiente para la observación i, x_{ki} es el valor que toma la variable k para la observación i, y e_i es el error del modelo.

Dado que el modelo se encuentra utilizando el método de mínimos cuadrados ordinarios (OLS) (se minimiza la suma de errores cuadrados e_i²), muchos se preguntan: ¿es OLS lo mismo que la regresión lineal? En realidad no, OLS simplemente es el nombre del método que nos permite encontrar la ecuación de la línea de regresión.

Las hipótesis de la regresión lineal son que los errores e_i siguen la misma distribución normal N(0,s) y son independientes.

Ir más allá: selección de variables en la regresión lineal

No todas las variables son importantes o significativas en el modelo de regresión lineal. Es posible seleccionar solo las más importantes utilizando uno de los cuatro métodos disponibles en XLSTAT:

• Mejor modelo: Este método permite seleccionar el mejor modo entre todos los modelos que pueden manejar un número de variables que varía de "Variables mínimas" a "Variables máximas". Además, el usuario puede elegir varios "criterios" para determinar el mejor modelo: R² ajustado, cuadrado medio de los errores (MSE), Cp de Mallows, AIC de Akaike, SBC de Schwarz, PC de Amemiya.
• El proceso de selección comienza añadiendo la variable con la mayor contribución al modelo (el criterio utilizado es el estadístico t de Student). Si una segunda variable es tal que la probabilidad asociada a su t es menor que la "Probabilidad de entrada", se añade al modelo. Lo mismo ocurre con una tercera variable. Una vez añadida la tercera variable, se evalúa el impacto de la eliminación de cada variable presente en el modelo después de haberla añadido (siempre utilizando el estadístico t). Si la probabilidad es mayor que la "Probabilidad de eliminación", se elimina la variable. El procedimiento continúa hasta que no se puedan añadir o eliminar más variables.
• Hacia adelante: El procedimiento es el mismo que para la selección por pasos, excepto que las variables solo se añaden y nunca se eliminan.
• Hacia atrás: El procedimiento comienza añadiendo simultáneamente todas las variables. A continuación, las variables se eliminan del modelo utilizando el mismo procedimiento que para la selección por pasos.

¿Cómo validar los supuestos de la regresión lineal?

Hay que verificar dos supuestos principales de la regresión lineal en relación con los residuos:

• deben seguir una distribución normal
• deben ser independientes

Utilice las distintas pruebas que aparecen en los resultados de la regresión lineal para comprobar a posteriori que las hipótesis subyacentes se han verificado correctamente.

La normalidad de los residuos puede comprobarse analizando ciertos gráficos o ejecutando un test de Shapiro-Wilk sobre los residuos. Para ello, es necesario activar la prueba correspondiente en la sub pestaña Supuestos de prueba.

La independencia de los residuos puede comprobarse analizando determinados gráficos o utilizando la prueba de Durbin-Watson (en el menú Series temporales).

¿Cómo se corrige la heteroscedasticidad y la autocorrelación??

Como se ha mencionado anteriormente, la homoscedasticidad y la independencia de los términos de error son hipótesis clave en la regresión lineal, donde se supone que las varianzas de los términos de error son independientes e idénticamente distribuidas y se distribuyen normalmente.

XLSTAT permite corregir la heteroscedasticidad y la autocorrelación, que pueden darse con diferentes métodos como el estimador sugerido por Newey y West (1987).

PRUEBELO

¿Qué resultados de la regresión lineal puedo ver en XLSTAT?

• Resumen de la selección de variables: Cuando se ha elegido un método de selección, XLSTAT muestra el resumen de la selección. Para una selección por pasos, se muestran los estadísticos correspondientes a los diferentes pasos.

  Cuando se ha seleccionado el mejor modelo para un número de variables que varía de p a q, se muestra el mejor modelo para cada número o variables con los estadísticos correspondientes y el mejor modelo para el criterio elegido se muestra en negrita.

• Estadística de bondad de ajuste: En esta tabla se muestran las estadísticas relacionadas con el ajuste del modelo de regresión:

  • Observaciones: el número de observaciones utilizadas en los cálculos. En las fórmulas que se muestran a continuación, n es el número de observaciones.
  • Suma de pesos: la suma de los pesos de las observaciones utilizadas en los cálculos. En las fórmulas que se muestran a continuación, W es la suma de las ponderaciones.
  • DF: el número de grados de libertad del modelo elegido (correspondiente a la parte del error).
  • R²: el coeficiente de determinación del modelo. Este coeficiente, cuyo valor está comprendido entre 0 y 1, solo se muestra si la constante del modelo no ha sido fijada por el usuario. El R² se interpreta como la proporción de la variabilidad de la variable dependiente que es explicada por el modelo. Cuanto más se acerque R² a 1, mejor es el modelo. El problema de la R² es que no tiene en cuenta el número de variables utilizadas para ajustar el modelo.
  • R² ajustado: es el coeficiente de determinación ajustado del modelo. El R² ajustado puede ser negativo si el R² es cercano a cero. Este coeficiente solo se calcula si la constante del modelo no ha sido fijada por el usuario. El R² ajustado es una corrección del R² que tiene en cuenta el número de variables utilizadas en el modelo.
  • MSE: la media de los cuadrados de los errores (MSE).
  • RMSE: el cuadrado medio de los errores (RMSE) es la raíz cuadrada del MSE.
  • MAPE: el porcentaje medio de error absoluto.
  • DW: el estadístico de Durbin-Watson. Este coeficiente es el coeficiente de autocorrelación de primer orden y se utiliza para comprobar que los residuos del modelo no están autocorrelacionados, dado que la independencia de los residuos es una de las hipótesis básicas de la regresión lineal. El usuario puede consultar una tabla de estadísticas de Durbin-Watson para verificar si la hipótesis de independencia de los residuos es aceptable.
  • Cp: Coeficiente Cp de Mallows. Cuanto más se acerque el coeficiente Cp a p, menos sesgado estará el modelo.
  • AIC: Criterio de información de Akaike. Este criterio, propuesto por Akaike (1973), se deriva de la teoría de la información y utiliza la medida de Kullback y Leibler (1951). Es un criterio de selección de modelos que penaliza los modelos en los que la adición de nuevas variables explicativas no aporta suficiente información al modelo, información que se mide a través del MSE. El objetivo es minimizar el criterio AIC.
  • SBC: Criterio Bayesiano de Schwarz. Este criterio, propuesto por Schwarz (1978) es similar al AIC, y el objetivo es minimizarlo.
  • PC: Criterio de predicción de Amemiya. Este criterio, propuesto por Amemiya (1980) se utiliza, al igual que el R² ajustado, para tener en cuenta la parsimonia del modelo.
  • RMSE de Press: El estadístico de Press solo se muestra si se ha activado la opción correspondiente en el cuadro de diálogo. El RMSE de Press puede entonces compararse con el RMSE. Una gran diferencia entre ambos indica que el modelo es sensible a la presencia o ausencia de determinadas observaciones en el modelo.

• Tabla de SS de tipo I: se utiliza para visualizar la influencia que tiene la adición progresiva de variables explicativas en el ajuste del modelo, en lo que respecta a la suma de los cuadrados de los errores (SSE), la media de los cuadrados de los errores (MSE), la F de Fisher o la probabilidad asociada a la F de Fisher. Cuanto menor sea la probabilidad, mayor será la contribución de la variable al modelo, estando ya todas las demás variables en el modelo. Las sumas de los cuadrados en la tabla de tipo I siempre suman el SS del modelo. Nota: el orden de selección de las variables en el modelo influye en los valores obtenidos.

• Tabla de SS de Tipo III: se utiliza para visualizar la influencia que tiene la eliminación de una variable explicativa en el ajuste del modelo, manteniéndose todas las demás variables, en cuanto a la suma de los cuadrados de los errores (SSE), la media de los cuadrados de los errores (MSE), la F de Fisher o la probabilidad asociada a la F de Fisher. Nota: a diferencia de los SS de tipo I, el orden de selección de las variables en el modelo no influye en los valores obtenidos.

• Tabla de análisis de la varianza: se utiliza para evaluar el poder explicativo de las variables explicativas. Cuando la constante del modelo no se fija en un valor determinado, el poder explicativo se evalúa comparando el ajuste (por lo que respecta a los mínimos cuadrados) del modelo final con el ajuste del modelo rudimentario que solo incluye una constante igual a la media de la variable dependiente. Cuando se fija la constante del modelo, la comparación se realiza con respecto al modelo para el que la variable dependiente es igual a la constante que se ha fijado.

• Tabla de parámetros del modelo: muestra la estimación de los parámetros, el error estándar correspondiente, la t de Student, la probabilidad correspondiente, así como el intervalo de confianza.

• Ecuación del modelo: se muestra la ecuación del modelo para facilitar su lectura o reutilización.

• Tabla de coeficientes estandarizados: la tabla de coeficientes estandarizados se utiliza para comparar los pesos relativos de las variables. Cuanto mayor sea el valor absoluto de un coeficiente, más importante será el peso de la variable correspondiente. Cuando el intervalo de confianza en torno a los coeficientes normalizados tiene valor 0 (esto se puede ver fácilmente en el cuadro de coeficientes normalizados), el peso de una variable en el modelo no es significativo.

• Tabla de predicciones y residuos: la tabla de predicciones y residuos indica, para cada observación, su peso, el valor de la variable explicativa cualitativa, si solo hay una, el valor observado de la variable dependiente, la predicción del modelo, los residuos, los intervalos de confianza junto con la predicción ajustada si se han activado las opciones correspondientes en el cuadro de diálogo. Se muestran dos tipos de intervalo de confianza: un intervalo de confianza en torno a la media (correspondiente al caso en que la predicción se haría para un número infinito de observaciones con un conjunto de valores dados para las variables explicativas) y un intervalo en torno a la predicción aislada (correspondiente al caso de una predicción aislada para los valores dados para las variables explicativas). El segundo intervalo es siempre mayor que el primero, ya que la incertidumbre es mayor. Si se han seleccionado datos de validación, se muestran al final de la tabla.

• La tabla de diagnósticos de influencia muestra para cada observación, su peso, el residuo correspondiente, el residuo estandarizado (dividido por el RMSE), el residuo estudiado, el residuo eliminado, el residuo eliminado estudiado, el apalancamiento, la distancia de Mahalanobis, la D de Cook, el CovRatio, el DFFit, el DFFit estandarizado, las DFBetas (una por coeficiente del modelo) y las DFBetas estandarizadas.

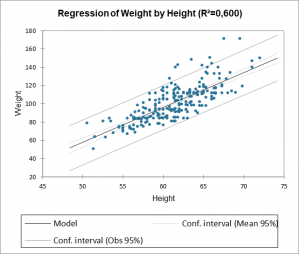
Por último, nuestro software XLSTAT le permite trazar la línea de regresión directamente en Excel. Puede controlar el error de regresión lineal gracias a los intervalos de confianza que también se muestran en el gráfico siguiente.