Analyse de Redondance (RDA)

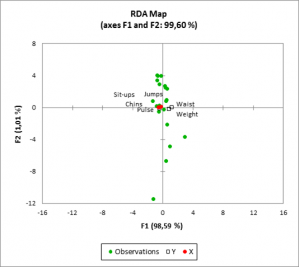
Utilité de l'analyse de redondance

L'Analyse de Redondance (RDA) a été développée par Van den Wollenberg (1977) comme alternative à l'Analyse Canonique des Corrélations (CCorA). L'Analyse de Redondance permet d'étudier la relation entre deux tableaux de variables Y et X. Tandis que la CCorA est une méthode symétrique, l'analyse de redondance est dissymétrique. Avec la CCorA, les composantes extraites des deux tableaux sont telles que leur corrélation est maximisée. Avec l'analyse de redondance, les composantes extraites à partir de X sont telles qu'elles sont autant que possible corrélés avec les variables de Y. Les composantes de Y sont ensuite extraites de telle sorte qu'elles soient autant que possible corrélées avec les composantes extraites de X.

Principe de l'Analyse de Redondance

Soit Y un tableau de variables réponse comprenant n observations et p variables. Ce tableau peut être analysé avec une analyse en composantes principales, afin d'obtenir une visualisation simultanée (biplot) des observations et des variables en deux ou trois dimensions. Soit X un second tableau correspondant aux mesures pour les mêmes n observations de q variables quantitatives et/ou qualitatives. L'analyse de redondance permet d'analyser la relation entre Y et X, et d'obtenir une représentation simultanée des observations, des variables réponse, et des variables explicatives en deux ou trois dimensions, optimale pour un critère de covariance (Ter Braak 1986).

L'analyse de redondance peut être décomposée en deux sous-parties :

1. une analyse sous contraintes dans un espace de dimension min(n-1, p, q). Cette partie est celle qui présente le plus d'intérêt car elle permet de relier l'analyse du tableau Y à X. Cette analyse est dénommée l'analyse de redondance contrainte
2. une analyse de la partie résiduelle, non contrainte, dans un espace de dimension min(n-1, p). Cette analyse est dénommée l'analyse de redondance non-contrainte.

Analyse de redondance partielle

L'analyse de redondance partielle ajoute une étape préliminaire. Le tableau X est subdivisé en deux groupes de variables : X(1) comprend des variables de conditionnement dont on veut supprimer l'effet, déjà connu ou sans intérêt pour l'étude. Des régressions de Y et X(2) par X(1) sont calculés, et les résidus de ces régressions sont ensuite utilisés pour l'analyse de redondance. L'analyse de redondance partielle permet donc d'étudier l'effet du second groupe de variables, sans que les variables du premier groupe ne viennent perturber l'analyse.

La terminologie Observations/Variables réponse/Variables explicatives a été choisie dans XLSTAT. Dans le cadre d'une étude en écologie, « Sites » pourrait être utilisé à la place d' « Observations », « Espèces » à la place de « Variables réponse », et « Variables environnementales » à la place de « Variables explicatives ».

Problématique des facteurs de mise à l'échelle (scaling) pour les biplots

XLSTAT propose trois types de mise à l'échelle. Le type de mise à l'échelle change la façon sont calculées dont les coordonnées (aussi appelés scores) des variables réponse et des observations, ce qui modifie par conséquent, leur position respective sur la représentation graphique. Soit u(ik) la coordonnée normalisée de la variable réponse i sur l'axe k, v(ik) la coordonnée normalisée de l'observation i sur l'axe k, L(k) la valeur propre correspondant à l'axe k, et T l'inertie totale (la somme des L(k) pour les RDA contrainte et non-contrainte). Les trois mises à l'échelle proposées dans XLSTAT, identiques à celles de vegan (un module pour le logiciel de R, Oksanen, 2007). Les u(ik) sont multipliés par c, et les v(ik) par d, et r est une constante définie par r = 4√(n-1)T, où n est le nombre d'observations.

Scaling 1: c = r √L(k)/T; d = r Scaling 2: c= r ; d =r √L(k)/T Scaling 3: c = d = r 4√L(k)/T

En plus des observations et des variables réponse, les variables explicatives peuvent être affichées sur le graphique. Les coordonnées de ces dernières sont obtenues en calculant les corrélations entre les variables du tableau X et les coordonnées des observations.

Résultats de l’analyse de redondance

Valeurs propres et pourcentages d'inertie : dans ces tableaux sont affichés pour l’analyse de redondance contrainte et l’analyse de redondance non contrainte, les valeurs propres, l'inertie associée, et les pourcentages correspondant, soit en terme d'inertie contrainte (ou non-contrainte), soit en terme d'inertie totale.

Les coordonnées (ou scores) des observations, des variables réponse et explicatives sont ensuite affichées. Ces coordonnées sont utilisées pour le graphique (simple, biplot ou triplot).

Le graphique permettent de visualiser la relation entre les observations, les variables réponse et explicatives. Lorsque des variables qualitatives ont été utilisées, les modalités correspondantes apparaissent en rouge avec un cercle évidé sur les graphiques. La légende les présente comme « modalités » afin de les différencier des autres variables explicatives.