Analyse Hiérarchique des Procédés (AHP)

Qu’est-ce que l'Analyse Hiérarchique des Procédés (AHP) ?

La méthode AHP est une méthode adaptée aux problèmes de décision multicritères c’est-à-dire comportant plusieurs solutions satisfaisant un ensemble de critères. L’approche de la méthode consiste à simplifier le problème en le décomposant en un système hiérarchique. Thomas Saaty est à l’origine de cette méthode et l’a créé dans les années 1970.

On appelle alternatives les solutions du problème décisionnel, critères les paramètres sur lesquels sont évaluées les alternatives, sous-critères les paramètres appartenant à un critère et sur lesquels sont évaluées les alternatives et évaluateur la personne qui va faire les évaluations. On parle d’un problème à 2 niveaux lorsqu’il admet des sous-critères, à l’inverse c’est un problème de niveau 1.

Options de la fonctionnalité AHP dans XLSTAT

Le principe de la méthode repose sur l’évaluation 2 à 2 des éléments du problème qui est regroupée dans des tableaux de comparaison. Ils sont définis à chaque niveau de la hiérarchisation. Au niveau 0 l’utilisateur définit le tableau de comparaison des critères, au niveau 1 ceux des sous-critères si c’est un problème à 2 niveaux sinon les tableaux de comparaison des alternatives sur les critères. Enfin, au niveau 2 on définit les tableaux de comparaison des alternatives sur les critères et/ou les sous-critères. L’ensemble de tous ces tableaux forme le plan d’expérience pour une analyse AHP.

XLSTAT met à votre disposition l’outil DHP pour créer votre plan d’expérience. Vous trouverez une déscription dans le menu Aide dans XLSTAT. 

Les tableaux de comparaison doivent être complétés par l’utilisateur en fonction de valeurs choisies dans le tableau de Saaty (plus d'info dans l'Aide de XLSTAT). Saaty a défini une échelle d’évaluation qui mesure l’importance ou la différence d’un élément sur un autre.

Les premiers calculs de la méthode AHP vont porter sur le calcul du vecteur des priorités à partir des valeurs du tableau de comparaison, c’est à dire le poids de chaque critère. La formule appliquée est la suivante :

Poids du critère = somme des lignes normalisées / nombre de critère

Avec la même formule, le vecteur des priorités des sous-critères est calculé pour chaque critère. Ce vecteur est ensuite pondéré par le poids du critère. On obtient ainsi les poids de chaque critère et des sous-critères qui interviendront dans la pondération des vecteurs priorités des alternatives calculées avec la même formule mathématique.

Une option dans les résultats de sortie est proposée pour évaluer la cohérence des données. Ce test permet de contrôler la saisie des valeurs dans les tableaux de comparaison. En effet si l’alternative A1 est évaluée 2 fois plus grande que l’alternative A2, et A2 est jugée 3 fois plus grande que l’alternative A3 et A3 4 fois plus grande que A1, alors le test permettra de dire qu’il y a une incohérence dans les données. On la mesure avec 2 paramètres : l’indice de cohérence (IC) et le ratio de cohérence (RC). La formule de calcul pour l’indice de cohérence est la suivante.

IC = cohérence moyenne - nombre d’éléments / (nombre d’éléments -1)

Le nombre d’éléments est le nombre de colonne ou de ligne du tableau de comparaison. Pour obtenir la cohérence moyenne on multiplie d’abord la matrice de comparaison avec son vecteur des priorités qui nous donne ainsi un nouveau vecteur. Puis, on divise ce dernier par le poids du vecteur priorité de l’élément de la même ligne. La moyenne de ce vecteur normé donne la cohérence moyenne. La formule pour le calcul du ratio de cohérence est donnée par :

RC = Indice de cohérence / cohérence aléatoire

Si le ratio de cohérence est inférieur ou égal à 10$%$ alors l’évaluation est jugée cohérente. A l’inverse, s’il est plus grand que 10$%$ il est recommandé de revoir l’évaluation du tableau de comparaison concerné.

Sorties de la fonctionnalité AHP dans XLSTAT

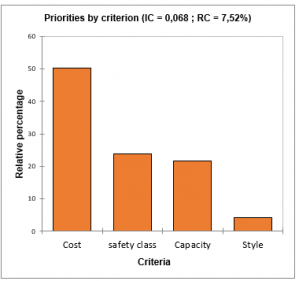
Priorités moyennes par critère : ce résultat, sous forme de tableau, correspond aux pourcentages relatifs moyens des vecteurs poids par critère sur l’ensemble des évaluateurs. Si les options « Diagrammes en bâton » et « critères » sont sélectionnées le résultat est aussi affiché sous forme de diagrammes en bâton en dessous du tableau.

Priorités moyennes par sous-critère : ce résultat, sous forme de tableau, correspond aux pourcentages relatifs moyens des vecteurs poids par sous-critère sur l’ensemble des évaluateurs. Si les options « Diagrammes en bâton » et « sous-critères » sont sélectionnées le résultat est aussi affiché sous forme de diagrammes en bâton en dessous des tableaux.

Priorités moyennes par alternatives : ce résultat, sous forme de tableau, correspond aux pourcentages relatifs moyens des vecteurs poids par alternatives sur l’ensembles des évaluateurs. Si l’option « Diagrammes en bâton » et « alternatives » sont sélectionnées le résultat est aussi affiché sous forme de diagrammes en bâton en dessous du tableau.

Résultats obtenus à partir des notes de l’évaluateur x : donnent l’ensemble des tableaux et des diagrammes en bâton pour l’évaluateur x en fonction des options cochées :

• Les priorités par critère : sont les pourcentages relatifs pour chaque critère.

• Les priorités par sous-critère du critère X : sont les pourcentages relatifs pour chaque sous-critère du critère X.

• Les priorités par alternative : sont les pourcentages relatifs pour chaque alternative.

Si l’option « Consistance des données » est activée les variables IC et RC sont calculées et affichées en dessous des tableaux (voir la section description pour plus de détails).