Analyse spectrale

Analyse spéctrale

La représentation spectrale d'une série chronologique Xt, (t=1,…,n), consiste en la décomposition de Xt en une sommes de sinusoïdes avec des coefficients aléatoires non corrélés. On peut en déduire une décomposition des fonctions de variance et d'autocovariance en une somme de sinusoïdes.

Densité spectrale

La densité spectrale correspond en théorie à la décomposition d'une série chronologique.

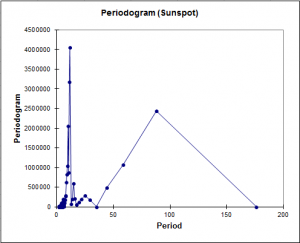
Cependant, dans la pratique, on n'a accès qu'à un nombre limité de données, échantillonnées en général à intervalles réguliers de temps. Pour cette raison, on doit dans un premier temps obtenir les coordonnées de la transformée de Fourier (partie réelle et partie imaginaire), puis le périodogramme, à partir duquel, grâce à une méthode de lissage on pourra obtenir une estimation de la densité spectrale qui est une meilleure représentation du spectre.

Enfin pour les noyaux XLSTAT propose :

• Bartlett
• Parzen
• Quadratic spectral
• Tukey-Hanning
• Tronqué

Analyse spetrale avec XLSTAT

XLSTAT calcule automatiquement les parties réelles et imaginaires pour chaque fréquence en s'appuyant sur des méthodes rapides et performantes de calcul de la transformation de Fourier.

Tests du bruit blanc

XLSTAT vous propose en option de calculer deux statistiques et la p-value associée, afin de déterminer si la série est significativement différente d'un bruit blanc ou non : le Kappa de Fisher et la statistique du Kolmogorov-Smirnov de Bartlett.