Analyse d'un plan de mélange

Description de l'analyse d'un plan de mélange

Description des modèles

L'analyse d'un plan de mélange se base sur le même principe qu'une régression linéaire. La différence majeure vient du modèle qui est utilisé. Plusieurs modèles sont utilisés.

Par défaut XLSTAT associe un modèle canonique réduit (Simplified Canonical Model) aux simplexes centrés. Toutefois, il est possible de changer de modèle sous réserve que le nombre de degrés de liberté soit suffisant (en augmentant le nombre de répétitions d'essais).

Afin de vérifier la contrainte associée au plan de mélange, on utilise un modèle polynomial sans constante. On différencie deux types de modèles, les modèles réduits et les modèles complets (à partir du degré 3).

Les modèles disponibles sont les suivants :

• Modèle linéaire (degré 1) 
• Modèle quadratique (degré 2)
• Modèle cubique complet (degré 3)
• Modèle cubique simplifié (spécial) 
• XLSTAT permet d'aller jusqu'au degré 4 (modèle quartique simplifié et complet).

L'estimation de ces modèles se fait par régression classique. 

Optimisation des réponses et désirabilité

Il est possible d'optimiser chaque réponse de manière individuelle et de combiner les résultats afin d'obtenir une fonction de désirabilité et d'analyser ses valeurs. Introduite par Derringer and Suich (1980), cette approche est basée sur la transformation de la réponse yi​ en une fonction de désirabilité individuelle di sur l'intervalle 0 ≤ di ​≤1.

Au moment de l'affichage, XLSTAT donne les 5 meilleures solutions trouvées lors de l'optimisation.

Sorties de l'analyse d'un plan de mélange dans XLSTAT

Information sur les variables : ce tableau récapitule les informations sur les facteurs. Pour chaque facteur, le nom court, le nom long et l'unité utilisée sont affichés.

Optimisation des réponses : ce tableau donne les 5 meilleures solutions obtenues lors de l'optimisation des réponses.

Matrice de corrélation : ce tableau est affiché afin de vous permettre d'avoir un aperçu des corrélations entre les différentes variables sélectionnées.

Coefficients d'ajustement : dans ce tableau sont affichées les statistiques relatives à l'ajustement du modèle de régression (Nombre d'observations, somme des poids, DDL, R2, R2 ajusté, MCE, RMCE, MAPE, coefficient de Durbin-Watson (DW), coefficient Cp de Mallows (Cp),  AIC, critère bayésien de Schwarz (SBC), critère de prédiction d'Amemiya (PC), statistique de Press, Q2).

Le tableau d'analyse de la variance permet d'évaluer le pouvoir explicatif des variables explicatives. 

Le tableau paramètres du modèle affiche l'estimation des paramètres, l'erreur type correspondante, le t de Student, la probabilité correspondante, ainsi que l'intervalle de confiance.

L'équation du modèle est ensuite affichée pour faciliter la lecture ou la réutilisation du modèle.

Le tableau des coefficients normalisés (aussi appelés coefficients bêta) permet de comparer le poids relatif des variables. Plus la valeur absolue d'un coefficient est élevée, plus le poids de la variable correspondante est important. Lorsque l'intervalle de confiance autour des coefficients normalisés comprend la valeur 0 (cela est facilement visible sur le graphique des coefficients normalisés), le poids d'une variable dans le modèle n'est pas significatif.

Dans le tableau des prédictions et résidus sont donnés pour chaque observation, son poids, la valeur de la variable explicative qualitative s'il n'y en a qu'une, la valeur observée de la variable dépendante, la prédiction du modèle, les résidus, les intervalles de confiance, ainsi que la prédiction ajustée et le D de Cook si les options correspondantes ont été activées dans la boîte de dialogue. 

Les graphiques qui suivent permettent de visualiser les résultats mentionnés ci-dessus. S'il n'y a qu'une seule variable explicative dans le modèle, le premier graphique affiché permet de visualiser les valeurs observées, la droite de régression et les deux types d'intervalles de confiance autour des prévisions. Le second graphique permet quant à lui de visualiser les résidus normalisés en fonction de la variable explicative. En principe, les résidus doivent être distribués de manière aléatoire autour de l'axe des abscisses. L'observation d'une tendance ou d'une forme révèlerait un problème au niveau du modèle.

Les trois graphiques affichés ensuite permettent de visualiser respectivement l'évolution des résidus normalisés en fonction de la variable dépendante, la distance entre les prédictions et les observations (pour un modèle idéal, les points seraient tous sur la bissectrice), et les résidus normalisés sous la forme d'un diagramme en bâtons. Ce dernier graphique permet de rapidement voir si un nombre anormal de données sort de l'intervalle ]-2, 2[]−2,2[ sachant que ce dernier, sous hypothèse de normalité, doit contenir environ 95% des données.

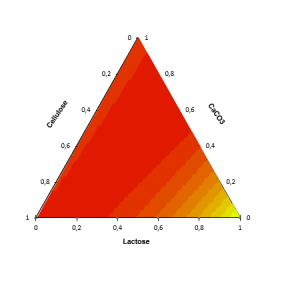
Graphe ternaire : pour chaque combinaison de facteurs, on trace un graphe ternaire. Ce graphe représente une surface de réponse sur une des faces du polyèdre que constitue le domaine expérimental. Ces graphiques facilitent l'interprétation du modèle et permettent d'identifier les configurations optimales.