ANOVA ou Analyse de la variance

Utilisez ce module pour réaliser une ANOVA (Analyse de variance) à un ou plusieurs facteurs, équilibrée ou déséquilibrée. Disponible dans Excel avec le logiciel XLSTAT.

Principes de l’ANOVA ou l’analyse de la variance

L'analyse de la variance (ANOVA) est une méthode utilisée pour partitionner la variance observée dans une variable particulière en composantes attribuables à différentes sources de variation.

Elle utilise le même cadre conceptuel que la régression linéaire. La principale différence vient de la nature des variables explicatives : au lieu d'être quantitatives, elles sont ici qualitatives. Dans l'ANOVA, les variables explicatives sont généralement appelées facteurs.

Dans XLSTAT, vous pouvez réaliser une ANOVA à un ou plusieurs facteurs, ou même une ANOVA à mesures répétées. Une ANOVA à un facteur comporte une seule variable explicative, tandis qu'une ANOVA à deux facteurs en comporte deux, et ainsi de suite. Dans tous les cas, l'hypothèse nulle de l'ANOVA est que la variance de la variable dépendante ne varie pas en fonction des modalités du ou des facteurs.

Si l'hypothèse nulle ne peut être acceptée, nous pouvons conclure que les facteurs influencent significativement les valeurs de la variable dépendante.

Vous ignorez si l'ANOVA est adaptée à vos données ? Vous souhaitez savoir quand utiliser une ANOVA ? Consultez notre guide pour choisir le bon outil de modélisation en fonction de votre situation.

Qu’est-ce que le modèle ANOVA?

Si p est le nombre de facteurs, le modèle de l'ANOVA s'écrit de la manière suivante :

y_i = β₀ + ∑_j=1...p β_{k_(i,j),j} + ε_i

où y_i est la valeur observée pour la variable dépendante pour l'observation i, k_(i,j) est l'indice correspondant à la modalité du facteur j pour l'observation i, et ε_i est l'erreur du modèle.

Le graphique ci-dessous montre des données qui peuvent être analysées à l'aide d'une ANOVA à un facteur. Le facteur a trois catégories. Les données sont des points orange. La ligne verte pointillée est la moyenne générale et les lignes vertes courtes sont les moyennes de chaque catégorie. Notez que nous utilisons arbitrairement la contrainte somme(ai)=0, ce qui signifie que β0 correspond à la moyenne générale.

Nous devons vérifier deux hypothèses principales dans l'ANOVA. Les hypothèses utilisées dans l'ANOVA sont identiques à celles utilisées dans la régression linéaire : les erreurs ε_{i,f} suivent la même distribution normale N(0,s) et sont indépendantes. Il est recommandé de vérifier rétrospectivement que les hypothèses sous-jacentes ont été correctement vérifiées. L'hypothèse de normalité des résidus peut être vérifiée en analysant certains graphiques sur les résidus ou grâce à un test de normalité. L'indépendance des résidus peut être vérifiée en analysant certains graphiques ou avec le test de Durbin Watson.

Sélection des données pour une analyse de variance dans XLSTAT

Pour réaliser une analyse dans XLSTAT, vous devez configurer vos données avec une variable par colonne.

Cependant, l'outil d'ANOVA de XLSTAT vous permet de sélectionner les données de deux manières différentes lorsque vous avez jusqu'à trois facteurs (variables explicatives) :

Sélectionner une seule colonne de valeurs pour chaque variable (dépendante et facteurs).
Sélectionner un tableau de données groupées où chaque ligne et chaque colonne correspondent à une modalité.

Options pour l’analyse de la variance ou ANOVA dans XLSTAT

XLSTAT permet de réaliser des ANOVA à un ou plusieurs facteurs. Des interactions jusqu'à l'ordre 4 peuvent être incluses dans le modèle ainsi que des effets imbriqués et aléatoires.
XLSTAT aide à réaliser des ANOVA équilibrées, mais également des ANOVA déséquilibrées.
XLSTAT a un dispositif automatique pour trouver les facteurs imbriqués. Un facteur imbriqué peut être inclus dans le modèle.
Des facteurs aléatoires peuvent être inclus dans une analyse ANOVA. Lorsque certains facteurs sont supposés être aléatoires, XLSTAT affiche le tableau des moyennes quadratiques attendues.
Quatre méthodes sont proposées pour sélectionner un modèle : Meilleur modèle, Régression pas-à-pas (ascendante, descendante, dans les deux sens).
Hypothèses de test : un test de Shapiro-Wilk est effectué sur les résidus. Un test de Levene est disponible pour tester l'homogénéité des variances. Le test est exécuté pour comparer chaque facteur et la variance des différentes catégories.

Comment vérifier les hypothèses de l'ANOVA, lorsque les conditions de l'ANOVA ne sont pas remplies ?

XLSTAT permet de corriger l'hétéroscédasticité et l'autocorrélation potentielles en utilisant plusieurs méthodes comme l'estimateur proposé par Newey et West (1987).

L'homoscédasticité et l'indépendance des termes d'erreur sont des hypothèses clés en régression linéaire ainsi qu’en ANOVA où l'on suppose que les variances des termes d'erreur sont indépendantes, identiquement distribuées et normalement distribuées. Lorsque ces hypothèses ne sont pas respectées (un test de Durbin Watson ou de White disponible dans le menu Séries temporelles permet de les vérifier), la matrice de covariance ne peut pas être estimée à l'aide de la formule classique. La variance des paramètres correspondant aux coefficients du modèle linéaire peut donc être erronée ainsi que leurs intervalles de confiance. Un prédicteur peut alors être considéré comme significatif (ou non), contrairement à la réalité. XLSTAT permet de corriger l'hétéroscédasticité et l'autocorrélation qui peuvent apparaître, notamment dans les séries temporelles.

Concernant l'hétéroscédasticité, White (1980), suivi par plusieurs auteurs, a exploré comment corriger l'estimation classique des covariances. Pour cela, il utilise les résidus et les effets de levier centrés obtenus à partir des calculs de régression linéaire (voir MacKinnon (1985) et Zeileis (2006)).

Tests de comparaisons multiples (post-hoc tests) après l'ANOVA

L'une des principales applications de l'ANOVA est le test de comparaisons multiples dont le but est de vérifier si les paramètres des différentes catégories d'un facteur diffèrent significativement ou non. Par exemple, dans le cas où quatre traitements sont appliqués à des plantes, nous voulons savoir non seulement si les traitements ont un effet significatif, mais également si les traitements ont des effets différents.

De nombreux tests ont été proposés pour comparer les moyennes des groupes. La majorité de ces tests supposent que l'échantillon est normalement distribué.

Résultats pour l’analyse de la variance dans XLSTAT

Les résultats renvoyés par l’ANOVA sont une analyse des résidus, les paramètres des modèles, l'équation du modèle, les coefficients normalisés, les sommes des carrés de type I et de type III, ainsi que les prédictions.

En outre, plusieurs méthodes de comparaison multiple, également appelées tests post-hoc, peuvent être exécutées en option : Test t corrigé de Bonferroni et Dunn-Sidak, test HSD de Tukey, test LSD de Fisher, test de Duncan, méthode de Newman-Keuls (SNK) et méthode REGWQ. Le test de Dunnett est aussi disponible pour permettre aux utilisateurs d'effectuer des comparaisons multiples avec le contrôle (MCC) et des comparaisons multiples avec le meilleur (MCB). Le test de Games-Howell (GH) peut être utilisé dans les ANOVA à sens unique lorsque les variances ne sont pas homogènes. Bien qu'il puisse être utilisé avec des tailles d'échantillon inégales, il est recommandé de l'utiliser quand le plus petit échantillon compte cinq éléments ou plus, sinon, il est trop libéral.

De plus, des diagnostics d'influence sont affichés pour chaque observation : le résidu, le résidu standardisé (divisé par le RMSE), le résidu studentisé, le résidu supprimé, le résidu supprimé studentisé, le levier, la distance de Mahalanobis, le D de Cook, le CovRatio, le DFFit, le DFFit standardisé, le DFBetas (un par coefficient de modèle) et le DFBetas standardisé.

Graphiques proposés dans l'analyse de la variance dans XLSTAT

Graphique des coefficients standardisés : le graphique en barres affiche les valeurs et les intervalles de confiance des coefficients standardisés.

Graphique de régression : le graphique montre les valeurs observées, la ligne de régression et les deux types d'intervalle de confiance autour des prédictions.
Résidus standardisés en fonction des prédictions du modèle : en principe, les résidus doivent être distribués de façon aléatoire autour de l'axe des X. S'il y a une tendance ou une forme, cela révèle un problème avec le modèle.

La distance entre les prédictions et les observations : pour un modèle idéal, les points sont tous sur la bissectrice.
Les résidus standardisés sur un diagramme à barres : ce dernier graphique permet de voir rapidement si un nombre anormal de valeurs se trouvent en dehors de l'intervalle [-2, 2[ puisque ce dernier, en supposant que l'échantillon soit normalement distribué, doit contenir environ 95 % des données.

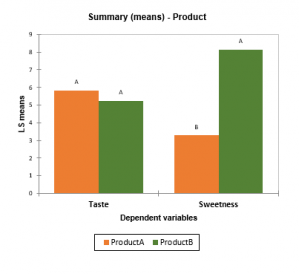
Graphiques récapitulatifs : si plusieurs variables dépendantes ont été sélectionnées et si l'option de comparaisons multiples a été activée, un graphique permet de visualiser les moyennes estimées avec des lettres de regroupement de comparaisons multiples.