Régression logistique pour réponse binaires et multinomiales (Logit, Probit, ...)

Définition de la régression logistique dans XLSTAT

Principes de la régression logistique

La régression logistique est une méthode très utilisée car elle permet de modéliser des variables binomiales (typiquement binaires), multinomiales (variables qualitatives à plus de deux modalités) ou ordinales (variables qualitatives dont les modalités peuvent être ordonnées). Elle est très utilisée dans le domaine médical (guérison ou non d'un patient), en sociologie, en épidémiologie, en marketing quantitatif (achat ou non de produits ou services suite à une action) et en finance pour la modélisation de risques (scoring).

Le principe du modèle de la régression logistique est d'expliquer la survenance ou non d'un événement (la variable dépendante notée Y) par le niveau de variables explicatives (notées X). Par exemple, dans le domaine médical, on cherche à évaluer à partir de quelle dose d'un médicament, un patient sera guéri.

Modèles de la régression logistique

Cas de la régression logistique pour des variables réponse binomiales

La régression logistique et la régression linéaire appartiennent à la même famille des modèles GLM (Generalized Linear Models) : dans les deux cas, on relie un événement à une combinaison linéaire de variables explicatives.

Dans le cas de la régression linéaire ordinaire, la variable dépendante Y suit une loi normale N(μ,σ) où μ est une fonction linéaire des variables explicatives. Pour la régression logistique binomiale, la variable dépendante, aussi appelée variable réponse, suit une loi de Bernoulli de paramètre p (p étant la probabilité pour que l'événement se produise), lorsque l'expérience est répétée une fois, ou une loi Binomiale(n, p) si l'expérience est répétée n fois (par exemple la même dose est essayée sur n insectes). Dans le cas de la régression logistique, le paramètre de probabilité p est une fonction d'une combinaison linéaire des variables explicatives X.

XLSTAT nomme "binaire" le cas où la variable réponse peut prendre 2 valeurs (correspondant à un tirage de Bernoulli), et "somme de binaires" le cas où la variable réponse est le comptage du nombre de fois où l'événement d'intérêt s'est produit.

Les fonctions les plus couramment utilisées pour relier la probabilité p aux variables explicatives sont la fonction logistique (on parle alors de modèle Logit) et la fonction de répartition de la loi normale standard (on parle alors de modèle Probit). Ces deux fonctions sont parfaitement symétriques et sigmoïdes. XLSTAT propose deux autres fonctions : la fonction Log-log complémentaire qui n'est plus symétrique car concentrée sur l'asymptote supérieure, et la fonction de Gompertz qui est au contraire plus concentrée sur l'axe des abscisses.

Dans la plupart des logiciels, le calcul des intervalles de confiance sur les paramètres est comme pour la régression linéaire basé une hypothèse de normalité des paramètres. XLSTAT propose aussi la méthode alternative LR ( likelihood ratio ) introduite par Venzon et Moolgavkar (1988). Cette méthode est plus fiable car elle ne nécessite pas de supposer la normalité des paramètres ; elle peut néanmoins ralentir les calculs car elle est itérative.

Cas de la régression logistique multinomiale

Le principe de la régression logistique multinomiale est d'expliquer ou de prédire une variable pouvant prendre J valeurs alternatives (les J modalités de la variable), en fonction de variables explicatives. Le cas binomial vu précédemment en est donc un cas particulier.

Dans le cadre du modèle multinomial, une modalité de référence doit être sélectionnée. Dans l'interface de XLSTAT elle est appelée « modalité témoin ». Idéalement, on choisira ce qui correspond à la situation "de base" ou "classique" ou "normale". Les coefficients estimés seront interprétés en fonction de cette modalité de référence. Pour la simplicité de l'écriture, les équations ci-dessous sont écrites en considérant que la première modalité comme modalité de référence.

Le modèle proposé par XLSTAT pour relier la probabilité de survenance d'un événement aux variables explicatives est le modèle logit qui est l'un des quatre modèles proposés pour le cas binomial. 

Contrairement à la régression linéaire, une solution analytique exacte n'existe pas. Il est donc nécessaire d'utiliser un algorithme itératif. XLSTAT utilise un algorithme de Newton-Raphson.

Cas de la régression logistique ordinale

Le principe de la régression logistique ordinale est d'expliquer ou de prédire une variable pouvant prendre J valeurs alternatives ordonnées (seul l'ordre importe, pas les écarts), en fonction de variables explicatives. La régression logistique binomiale est un cas particulier de la régression logistique ordinale, correspondant au cas où J=2.

XLSTAT permet d'utiliser deux modèles alternatifs pour calculer les probabilités d'affectation aux modalités à partir des variables explicatives : le modèle logit et le modèle probit.

Contrairement à la régression linéaire, une solution analytique exacte n'existe pas. Il est donc nécessaire d'utiliser un algorithme itératif. XLSTAT utilise un algorithme de Newton-Raphson.

Résultats de la régression logistique dans XLSTAT

XLSTAT propose un nombre important de tableaux et de graphiques afin de faciliter l'analyse et l'interprétation des résultats.

Statistiques descriptives : le tableau de statistiques descriptives présente pour toutes les variables sélectionnées des statistiques simples. Pour les variables quantitatives sont affichés le nombre d'observations, le nombre de données manquantes, le nombre de données non manquantes, la moyenne et l'écart-type (non biaisé). Pour les variables qualitatives, dont la variable dépendante, sont affichées les modalités, leurs effectifs et pourcentage respectifs.

Matrice de corrélation : dans ce tableau sont affichées les corrélations entre les variables explicatives. Il est à noter que si la variable dépendante est binaire, le coefficient de corrélation bisérielle est utilisé pour calculer la corrélation entre les variables explicatives quantitatives et la variable dépendante.

Synthèse de la sélection des variables : dans le cas où une méthode de sélection a été choisie, XLSTAT affiche la synthèse de la sélection. Dans le cas d'une sélection pas à pas, les statistiques correspondant aux différentes étapes sont affichées. Dans le cas d'une sélection du meilleur modèle pour un nombre de variables variant de p à q, le meilleur modèle pour chaque nombre de variable est affiché avec les statistiques correspondantes ; le meilleur modèle pour le critère choisi est alors affiché en gras.

Coefficients d'ajustement : dans ce tableau est affichée une série de statistiques pour le modèle indépendant (correspondant au cas où la combinaison linéaire des variables explicatives se réduit à une constante) et pour le modèle ajusté.

• Observations : le nombre total d'observations prises en compte (somme des poids des observations) ;

• Somme des poids : le nombre total d'observations prises en compte (somme des poids des observations multipliée par les poids dans la régression) ;

• DDL : degrés de liberté ;

• -2 Log(Vrais.) : le logarithme de la fonction de vraisemblance associée au modèle;

• R² (McFadden) : coefficient compris comme le R² entre 0 et 1 qui mesure le bon ajustement du modèle. Ce coefficient est égal à 1 moins le rapport de la vraisemblance du modèle ajusté sur la vraisemblance du modèle indépendant ;

• R²(Cox et Snell) : coefficient compris comme le R² entre 0 et 1 qui mesure le bon ajustement du modèle. Ce coefficient est égal à 1 moins le rapport de la vraisemblance du modèle ajusté sur la vraisemblance du modèle indépendant, le rapport étant porté à l'exposant 2/Sw, où Sw est la somme des poids ;

• R²(Nagelkerke) : coefficient compris comme le R² entre 0 et 1 qui mesure le bon ajustement du modèle. Ce coefficient est égal au rapport du R² de Cox et Snell, divisé par 1 moins la vraisemblance du modèle indépendant portée à l'exposant 2/Sw ;

• AIC : le critère d'information d'Akaike (Akaike's Information Criterion) ;

• SBC : le critère bayésien de Schwarz (Schwarz's Bayesian Criterion).

Test de l'hypothèse nulle H0 : Y=p0 : l'hypothèse H0 correspond au modèle indépendant qui donne la probabilité p0 quelques soient les valeurs des variables explicatives ; on cherche à vérifier si le modèle ajusté est significativement plus performant que ce modèle. Trois tests sont proposés : le test du rapport des vraisemblance (-2 Log(Vrais.)), le test du Score, et le test test de Wald. Les trois statistiques suivent une loi du chi2 dont les degrés de liberté sont indiqués.

Analyse de Type II : ce tableau n'a d'intérêt que s'il y a plus d'une variable explicative. On teste ici le modèle ajusté contre un modèle dont on aurait retiré la variable de la ligne du tableau en question. Si la probabilité Pr>LR est inférieure à un seuil de signification que l'on se fixe (typiquement 0.05), alors la contribution de la variable à l'ajustement du modèle est significative. Sinon, elle peut être retirée du modèle.

Paramètres du modèle :

• Cas binaire : pour la constante du modèle et pour chaque variable explicative sont affichés l'estimation du paramètre, l'écart-type correspondant, le chi2 de Wald, la p-value correspondante, ainsi que l'intervalle de confiance. Si l'option correspondante a été activée, les intervalles LR (Likelihood Ratio) sont aussi affichés. L'odds ratio et l'intervalle de confiance associé sont affichés dans la partie droite du tableau.

• Cas Multinomial : dans le cas multinomial, on obtient une série de coefficients pour chaque modalité active. On aura donc (J-1)(q+1) lignes dans le tableau où J est le nombre de modalités de la variable dépendante et q est le nombre de variables explicatives. Ainsi, pour chaque variable et pour chaque modalité sont affichés l'estimation du paramètre, l'écart-type correspondant, le chi2 de Wald, la p-value correspondante, l'intervalle de confiance, l'odds ratio et l'intervalle de confiance associé.

• Cas ordinal : dans le cas ordinal, on obtient une constante pour chaque modalité et une seule série de coefficients. On aura donc (J-1)+q lignes dans le tableau où J est le nombre de modalités de la variable cible et q est le nombre de variables explicatives. Ainsi, pour chaque variable et pour chaque modalité sont affichés l'estimation du paramètre, l'écart-type correspondant, le chi2 de Wald, la p-value correspondante et l'intervalle de confiance.

Les équations du modèle sont ensuite affichées pour faciliter la lecture ou la réutilisation du modèle.

Le tableau des coefficients normalisés (aussi appelés coefficients bêta) permet de comparer le poids relatif des variables. Plus la valeur absolue d'un coefficient est élevée, plus le poids de la variable correspondante est important. Lorsque l'intervalle de confiance autour des coefficients normalisés comprend la valeur 0 (cela est facilement visible sur le graphique des coefficients normalisés), le poids d'une variable dans le modèle n'est pas significatif.

Les effets marginaux au point correspondant aux moyennes des variables explicatives sont alors affichées. Les effets marginaux sont particulièrement intéressants lorsqu'ils sont comparés les uns aux autres. En les comparant, on peut mesurer l'impact relatif de chaque variable au point donné. L'impact peut être interprété comme l'influence d'une petite variation de chaque variable explicative, sur la variable dépendante. Un intervalle de confiance calculé à l'aide de la méthode Delta est affiché. XLSTAT fournit ces résultats pour les variables quantitatives et qualitatives, qu'il s'agisse de facteurs simples ou d'interactions. Pour les variables qualitatives, l'effet marginal indique l'impact d'un changement de modalité (de la première modalité à la modalité d'intérêt).

Dans le tableau des prédictions et résidus sont donnés pour chaque observation, son poids, la valeur de la variable explicative quantitative (s'il n'y en a qu'une), la valeur observée de la variable dépendante, la prédiction du modèle, les mêmes valeurs divisées par le poids dans le cas somme(binaires), les probabilités associées à chaque modalité. Dans le cas binaire, l'intervalle de confiance associé aux probabilités est affiché. Si la modalité prédite est différente de celle observée, il est indiqué si cela est significatif ou non. Il est également indiqué si la probabilité associée à la probabilité maximale est significativement différente des autres.

Le tableau des diagnostics d'influence permet de d'évaluer l'impact de chaque observation sur la qualité du modèle ou sur la valeur des coefficients du modèle.

Tableau de classification : activez cette option pour afficher le tableau permettant de visualiser le pourcentage d'observations bien classées pour chacune des deux catégories. Si un échantillon de validation a été extrait, ce tableau est aussi affiché pour les données de validation.

Courbe ROC : la courbe ROC permet d'évaluer la performance du modèle au travers de l'aire sous la courbe (AUC) et de comparer plusieurs modèles entre eux. Elle n'est affichée que dans le cas binaire.

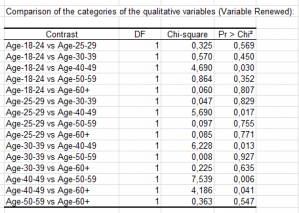
Comparaison des modalités des variables qualitatives : si une ou plusieurs variables qualitatives explicatives ont été sélectionnées, les résultats des tests d'égalité des paramètres pris deux à deux des différentes modalités des variables qualitatives sont affichés.

Le tableau d'analyse des probabilités n'est affiché que si une seule variable explicative quantitative a été sélectionnée et si l'on est dans le cas binomial. Il permet de visualiser à quel niveau de la variable explicative correspond une probabilité donnée.