Plans d'expérience pour l'analyse sensorielle

Utilité des plans d’expérience en analyse sensorielle

La planification expérimentale est une étape fondamentale pour quiconque veut s'assurer que les données collectées seront exploitables dans les meilleures conditions statistiques possibles. Rien ne sert de faire évaluer des produits par un panel de sujets si l'on ne peut ensuite comparer les produits dans des conditions statistiques satisfaisantes. Il n'est par ailleurs pas nécessaire de faire évaluer tous les produits par tous les sujets pour pouvoir comparer les produits entre eux.

Cet outil a pour but de permettre aux spécialistes de l'analyse sensorielle de disposer d'un outil simple et puissant pour mettre en place une étude sensorielle menée auprès de sujets (experts et/ou consommateurs) évaluant un ensemble de produits.

Exemple de plan d’expérience et exigences en analyse sensorielle

Lorsque l'on veut faire évaluer par exemple 9 produits par un panel de consommateurs, se pose dans un premier temps la question du nombre de consommateurs à faire intervenir, sachant qu'il peut exister des contraintes techniques (on n'a accès qu'à un nombre limité de consommateurs entrainés) ou des contraintes budgétaires. Une fois le nombre de consommateurs arrêté, par exemple 82, se pose la question du nombre maximum de produits que peut évaluer un consommateur à chaque session, rarement pour des raisons budgétaires, mais plus souvent en raison de contraintes physiologiques : un consommateur, même entrainé, ne peut pas nécessairement garder toutes ses capacités sensorielles s'il évalue trop de produits à la suite. Imaginons que l'expérience montre que trois produits est un maximum pour une session et que pour des raisons d'organisation, seules deux sessions peuvent être organisées. Chaque consommateur évaluera donc au maximum 6 produits.

Reste maintenant à déterminer quels produits seront évalués par chacun des 82 consommateurs, au cours de chaque session, et dans quel ordre. Il est possible que l'ordre ait une influence (ce n'est pas le sujet ici, mais un plan d'expérience pourrait permettre dans une autre étude de vérifier ou invalider cette hypothèse). Afin d'éviter que certains produits soient pénalisés, il faut donc de faire en sorte que les produits soient vus aussi souvent que possible dans les 3 positions possibles au cours de chaque session. Par ailleurs, il est possible que certains enchainements de produits aient aussi une influence sur les appréciations sensorielles. On se limite ici à considérer les couples ordonnés de produits (carry-over d'ordre 2). Comme pour l'ordre, on veillera aussi à ce que les différents couples ordonnés, 72 dans notre exemple, soient présents avec une fréquence aussi homogène que possible dans le plan d'expériences.

La génération du plan va donc essayer de concilier la triple exigence suivante :

• Les produits doivent être vus par autant de sujets que possible et avec une fréquence globale pour les différents produits aussi homogène que possible,
• Chaque produit doit être vu dans les différentes positions au cours de chaque session, avec une fréquence globale pour chaque couple (position, produit) aussi homogène que possible
• Les différents couples ordonnés de produits doivent être présents dans le plan d'expériences avec une fréquence aussi homogène que possible.

Mesure de la performance du plan d’expérience

Appelons N la matrice ayant autant de lignes que de produits et autant de colonnes que de sujets, et contenant le nombre de fois où chaque sujet voit chaque produit au cours de chaque session. Dans les plans sensoriels que nous traitons ici, N contient soit des 0, soit des 1 : on impose qu'un sujet voit chaque produit au maximum une fois. Par ailleurs les sommes marginales par colonnes sont constantes et égales à k (le nombre de produits vus par chaque sujet est imposé). La matrice M=NN' a la particularité de comporter sur sa diagonale la fréquence de chaque produit dans le plan, et sur les parties triangulaires inférieures et supérieures le nombre de fois où des sujets ont évalué chaque couple de produits (ici l'ordre n'importe pas). On l'appelle matrice de cooccurrence (concurrence matrix en anglais).

Soit la matrice A*=I-qNN'q/k où q est une matrice diagonale comportant l'inverse de la racine carrée de la fréquence de chaque produit. On montre que cette matrice est directement liée à la matrice d'information concernant les produits et donc aux variances et covariances des paramètres associés aux produits dans un modèle d'ANOVA que l'on pourra calculer une fois les évaluations recueillies. Si l'on veut s'assurer que les variances des différences entre les paramètres associés aux produits soient aussi homogènes que possible, on montre qu'il faut faire en sorte que les valeurs propres de la matrice A* soit aussi proches les unes des autres.

On définit la A-efficacité comme la moyenne harmonique des, au plus p-1, valeurs propres non nulles de la matrice A*, et la D-efficacité comme la moyenne géométrique des mêmes valeurs propres. Les deux critères sont égaux dans le cas idéal où toutes les valeurs propres sont égales.

Plans d’expérience en blocs incomplets équilibrés

Un plan en blocs est un plan d'expériences dans lequel on étudie l'influence d'au moins deux facteurs sur un ou plusieurs phénomènes. On sait que l'un des facteurs a par construction un effet important, sans que l'on puisse agir dessus, mais ce n'est pas celui qui nous intéresse. On veut donc pouvoir s'assurer que ce facteur ne perturbera pas les analyses que l'on effectuera une fois les données collectées. Pour cela on fait en sorte que les différents niveaux des autres facteurs soient aussi bien représentés dans chacun des blocs (les modalités du facteur bloc) .

Dans notre cas, nous avons un facteur bloc qui correspond aux sujets, et un facteur que l'on souhaite particulièrement étudié, le facteur produit. Un plan en blocs complets est un plan dans lequel tous les niveaux des facteurs étudiés sont présents une fois à l'intérieur de chaque bloc. Cela correspond, pour un plan sensoriel, au cas où tous les produits sont vus une fois par l'ensemble des sujets. Un plan en blocs incomplets est un plan dans lequel tous les niveaux des facteurs étudiés ne sont pas présents dans chaque bloc. Il est équilibré si chaque niveau de chaque facteur étudié est présent un même nombre r de fois et si chaque couple de niveaux de chaque facteur étudié est présent un même nombre de fois λ.

Si v est le nombre de produits étudiés, b le nombre de sujets, k le nombre de produits vus par chaque sujet, on montre que les conditions suivantes sont nécessaires (mais non suffisantes) pour avoir un plan en blocs incomplets équilibrés :

bk=vr r(k-1)= λ(v-1)

Dans le cas où un plan en blocs incomplets équilibrés existe, on connaît la valeur optimale des deux critères (A et D-efficacité). Cette valeur est donnée par XLSTAT permet de chercher un plan optimal au sens de la A- efficacité ou de la D- efficacité tant dans le cas des plans complets que dans le cas des plans en blocs incomplets, qu'ils soient équilibrés ou non.

Algorithmes de recherche du plan d’expérience

XLSTAT s'appuie sur deux techniques différentes pour générer les plans. Si l'option rapide est choisie par l'utilisateur et si (b/v) est entier, alors XLSTAT utilise la méthode des plans cycliques introduite par Williams (1949), et étudiée très en détail par John et Williams (1995). Si (b/v) n'est pas entier ou si l'option de calcul rapide n'est pas demandée, XLSTAT utilise une méthode propriétaire (non publiée) très performante permettant de générer très vite une solution pertinente et à partir de cette solution, de chercher par recuit simulé une meilleure solution, pendant un temps maximal fixé par l'utilisateur. Si le plan recherché est un plan en blocs complets ou incomplets équilibrés et que l'optimum est trouvé, la recherche de plan s'interrompt avant que le temps imparti soit écoulé.

Algorithmes d'amélioration des fréquences des positions et du carry-over

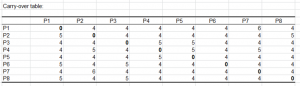
Une fois le plan trouvé (la matrice N est dorénavant connue), reste à ordonner les produits de façon à optimiser le plan sensoriel (Périnel et Pagès, 2004). On veut notamment que chaque produit se trouve un nombre de fois égal à chaque rang et que chaque couple ordonné de produits se retrouve un nombre égal de fois. XLSTAT va se servir pour cela de deux matrices : la matrice des fréquences des positions et la matrice du carry-over. Le but de l'algorithme sera de rendre le plus homogène possible ces matrices. La matrice de carry-over est une matrice qui fait apparaître à la position ij le nombre de fois que le produit i précède le produit j dans le plan. On définit un paramètre l qui va nous permettre de favoriser soit l'obtention d'un bon carry-over (l proche de 0) soit l'obtention d'une matrice des fréquences de positions le plus proche de la matrice constante (l proche de 1).

L'algorithme d'optimisation est itératif et consiste en des permutations des rangs des produits associés à chaque sujet de façon à optimiser le critère suivant : λ Σ_i,j r_ij² + (1 – λ) Σ_i,j s_ij² Où les r_ij sont les éléments de la matrice des fréquences des positions et les s_ij, les éléments de la matrice de carry-over. Dès que l'optimum ou que le nombre maximum d'itérations sont atteints, l'algorithme s'arrête. XLSTAT utilise deux indices afin de vérifier la qualité de ces deux matrices :

• le MDR (mean deviation of R) : MDR = Σ_i,j (r_ij - r) Déviation par rapport à la moyenne des éléments de la matrice des fréquences des positions.
• le MDS (mean deviation of S): MDS = Σ_i,j (s_ij - s) Déviation par rapport à la moyenne des éléments de la matrice du carry-over.

Pour les plans en blocs incomplets équilibrés, on peut calculer la valeur optimale de ces indices ce qui permet de voir si le plan obtenu est optimal.

Plans d’expérience résolvables et présentation améliorée

Un plan résolvable est un plan qui peut être subdivisé en g groupes de sujets tels que qu'à l'intérieur de chaque groupe, on ait une occurrence de chaque produit. Certains plans en blocs incomplets équilibrés possèdent cette propriété. Présenter un plan avec une telle subdivision en groupes présente l'avantage que si certains sujets ne se présentent pas, il n'est pas nécessaire de reconstruire un plan d'expériences, mais simplement de faire en sorte que les expériences annulées soient les dernières du plan. Cette approche est aussi particulièrement intéressante lorsque l'on veut mettre en place plusieurs sessions d'évaluation (voir ci-dessous). Une condition pour qu'un plan en blocs incomplets équilibrés soit résolvable est que v/k doit être un entier.

Même lorsqu'ils ne sont pas équilibrés ou résolvables, XLSTAT cherche à présenter les plans en blocs incomplets de telle manière que les produits soient présents au plus deux fois et si possible une seule fois dans un groupe de taille (où vaut i si i est un entier, et l'arrondi à la valeur entière supérieure sinon). Ainsi, si des sujets étaient finalement absents, cela ne pénaliserait pas trop la qualité du plan tel qu'il a été initialement conçu.

Sessions pour le plan d’expérience

Il peut arriver que dans une expérimentation on ait trop de produits à tester par sujet et qu'il faille plusieurs sessions afin de ne pas saturer les sujets. Lorsque plusieurs sessions sont demandées, XLSTAT utilise le même plan initial pour chaque session, puis effectue une permutation des sujets et des positions à l'intérieur de groupes de sujets, à chaque session. Pour les plans résolvables, les groupes de sujets utilise des groupes de taille v/k. Ainsi, dans la mesure du possible, un même sujet n'évaluera pas deux fois le même produit d'une session à l'autre.